题目内容
11.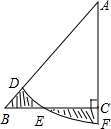 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$.
分析 若两个阴影部分的面积相等,那么△ABC和扇形ADF的面积就相等,可分别表示出两者的面积,然后列出方程即可求出AF的长度.
解答  解:∵图中两个阴影部分的面积相等,
解:∵图中两个阴影部分的面积相等,
∴S扇形ADF=S△ABC,即:$\frac{45π•A{F}^{2}}{360}$=$\frac{1}{2}$×AC×BC,
又∵AC=BC=1,
∴AF2=$\frac{4}{π}$.
故答案为:$\frac{4}{π}$.
点评 此题主要考查了扇形面积的计算方法及等腰直角三角形的性质,能够根据题意得到△ABC和扇形ADF的面积相等,是解决此题的关键,难度一般.

练习册系列答案
相关题目
16.在正三角形、平行四边形、矩形、菱形和圆这五个图形中,既是轴对称图形又是中心对称图形有( )
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
 如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?
如图所示,AB⊥BD于点B,CD⊥BD于点D,∠1+∠2=180°,试问CD与EF平行吗?为什么?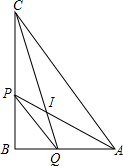 如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.
如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.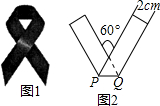 红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.
红丝带(图1)是对HIV和艾滋病认识的国际符号,1991年在美国纽约第一次出现,它代表了关心,这一标志被越来越多的人佩带,用来表示他们对HIV和艾滋病的关心.现将宽为2cm的长方形纸条折叠成如图2所示的丝带形状,那么折痕PQ的长是$\frac{4\sqrt{3}}{3}$.