题目内容
3.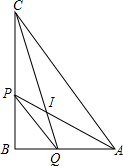 如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.
如图,在Rt△ABC中,∠B=90°,AP、CQ分别平分∠BAC、∠BCA,AP交CQ于I,连PQ,则S△IAC:S四边形ACPQ=1:2.
分析 在AC上截取CE=CP,AF=AQ,连接IE、IF,作FN⊥IE于N,QM⊥AI于M,只要证明△CIP≌△CIE,△IAF≌△IAQ,以及S△IMQ=S△INF即可解决问题.
解答 解: 在AC上截取CE=CP,AF=AQ,连接IE、IF,作FN⊥IE于N,QM⊥AI于M.
在AC上截取CE=CP,AF=AQ,连接IE、IF,作FN⊥IE于N,QM⊥AI于M.
在△CIP和△CIE中,
$\left\{\begin{array}{l}{CI=CI}\\{∠ICP=∠ICE}\\{CP=CE}\end{array}\right.$,
∴△CIP≌△CIE,同理△IAF≌△IAQ,
∴S△CIP=S△CIE,S△AIF=S△AIQ,PI=PE,IQ=IF,∠CIP=∠CIE,∠AIQ=∠F,
∵∠B=90°,IC平分∠ACB,IA平分∠BAC,
∴∠AIC=90°+$\frac{1}{2}$∠B=135°,
∴∠CIP=∠CIE=∠AIQ=∠EIF=45°,
在△IMQ和△INF中,
$\left\{\begin{array}{l}{∠INF=∠IMQ=90°}\\{∠NIF=∠QIM}\\{IF=IQ}\end{array}\right.$,
∴△INF≌△IMQ,
∴FN=QM,
∵S△IMQ=$\frac{1}{2}$•PI•QM,S△INF=$\frac{1}{2}$•IE•NF,
∴S△INF=S△IMQ,
∴S△AIC=S△CIE+S△EIF+S△IAF=$\frac{1}{2}$S四边形ACPQ.
故S△IAC:S四边形ACPQ=1:2.
故答案为1:2.
点评 本题考查角平分线的性质、全等三角形的判定和性质、三角形的面积公式等知识,添加辅助线是解决问题的关键,题目有难度,记住利用角平分线构造全等三角形的方法.

练习册系列答案
相关题目
15.下列调查中,最适合用普查方式的是( )
| A. | 调查某品牌牛奶质量合格率 | |
| B. | 调查某幼儿园一班学生的平均身高 | |
| C. | 调查某市中小学生收看纪念抗日战争胜利70周年大阅兵的情况 | |
| D. | 调查某省九年级学生一周内网络自主学习的情况 |
12.(-$\frac{1}{2}$)-2等于( )
| A. | -4 | B. | 4 | C. | -$\frac{1}{4}$ | D. | $\frac{1}{4}$ |
13.已知A(1,1)、B(3,2),点B绕点A逆时针旋转90°到达点C处,则点C的坐标是( )
| A. | (0,3) | B. | (-1,3) | C. | (3,-1) | D. | (3,0) |
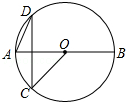 如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.
如图,AB是⊙O的直径,C、D是⊙O上两点,CD⊥AB,若∠DAB=65°,则∠OCD=40°.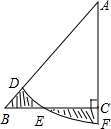 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF2为$\frac{4}{π}$. 如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.
如图,点C,E,F,B在同一直线上,点A,D在BC异侧,AB∥CD,AE=DF,∠A=∠D.求证:AB=CD.