题目内容
 如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.
如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交弧BC于D.(1)请写出五个不同类型的正确结论;
(2)若BC=12,ED=3,求⊙O的半径;
(3)若△BED∽△BCA,请你说明△OBD为等边三角形.
考点:垂径定理,勾股定理,圆周角定理,相似三角形的性质
专题:
分析:(1)AB是⊙O的直径,则AB所对的圆周角是直角,BC是弦,OD⊥BC于E,则满足垂径定理的结论;
(2)OD⊥BC,则BE=CE=
BC=6,在Rt△OEB中,由勾股定理就可以得到关于半径的方程,可以求出半径;
(3)证明△BEO≌△BED即可证得.
(2)OD⊥BC,则BE=CE=
| 1 |
| 2 |
(3)证明△BEO≌△BED即可证得.
解答:解:(1)不同类型的正确结论有:
①BE=CE;
②弧BD=弧DC;
③∠BED=90°;
④∠BOD=∠A;
⑤AC∥OD;
⑥AC⊥BC;
⑦OE2+BE2=OB2;
⑧S△ABC=BC•OE;
⑨△BOD是等腰三角形;
⑩△BOE∽△BAC…
(2)∵OD⊥BC,
∴BE=CE=
BC=6,
设⊙O的半径为R,则OE=OD-DE=R-3,
在Rt△OEB中,由勾股定理得: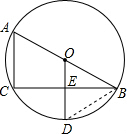 OE2+BE2=OB2,即(R-3)2+62=R2,
OE2+BE2=OB2,即(R-3)2+62=R2,
解得R=
,
∴⊙O的半径为
.
(3)∵△BED∽△BCA,
则在△BEO和△BED中,
,
∴△BEO≌△BED(ASA),
∴OB=BD,
∴OB=BD=OD,即△OBD是等边三角形.
①BE=CE;
②弧BD=弧DC;
③∠BED=90°;
④∠BOD=∠A;
⑤AC∥OD;
⑥AC⊥BC;
⑦OE2+BE2=OB2;
⑧S△ABC=BC•OE;
⑨△BOD是等腰三角形;
⑩△BOE∽△BAC…
(2)∵OD⊥BC,
∴BE=CE=
| 1 |
| 2 |
设⊙O的半径为R,则OE=OD-DE=R-3,
在Rt△OEB中,由勾股定理得:
 OE2+BE2=OB2,即(R-3)2+62=R2,
OE2+BE2=OB2,即(R-3)2+62=R2,解得R=
| 15 |
| 2 |
∴⊙O的半径为
| 15 |
| 2 |
(3)∵△BED∽△BCA,
则在△BEO和△BED中,
|
∴△BEO≌△BED(ASA),
∴OB=BD,
∴OB=BD=OD,即△OBD是等边三角形.
点评:本题主要考查了垂径定理,求圆的弦,半径,弦心距的长问题可以转化为解直角三角形的问题.

练习册系列答案
相关题目
 如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.
如图,P为Rt△ABC斜边AB的中点,过P作PQ∥AC,且PQ=AC.证明:△APQ是等腰三角形.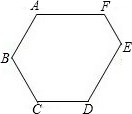 如图,在六边形ABCDEF中,AF∥CD,AB∥ED,∠A=140°,∠B=100°,∠E=90°.求∠C、∠D、∠F的度数.
如图,在六边形ABCDEF中,AF∥CD,AB∥ED,∠A=140°,∠B=100°,∠E=90°.求∠C、∠D、∠F的度数.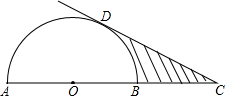 如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为
如图,AB是半圆O的直径,延长OB至点C,使BC=AO,过点C作半圆的切线,切点为D.如果半圆的半径为r,图中阴影部分的面积为S,则S可用r表示为