题目内容
7.已知二次函数y=x2-mx+4的图象与x轴交于A、B两点,且A、B两点间的距离为2.(1)求二次函数的解析式;
(2)求二次函数的最小值.
分析 (1)设A、B两点的坐标为(a,0),(b,0),则|a-b|=2,根据根与系数的关系得到a+b=m,ab=4,利用完全平方公式得到(a+b)2-4ab=4,则m2-4×4=4,然后解方程求出m即可得到抛物线解析式;
(2)把(1)中的解析式配成顶点式,然后根据二次函数的性质确定最小值.
解答 解:(1)设A、B两点的坐标为(a,0),(b,0),则|a-b|=2,
∵a、b是方程x2-mx+4的两根,
∴a+b=m,ab=4,
∵(a-b)2=4,
∴(a+b)2-4ab=4,
∴m2-4×4=4,解得m=2$\sqrt{5}$或-2$\sqrt{5}$,
∴抛物线解析式为y=x2-2$\sqrt{5}$x+4或y=x2+2$\sqrt{5}$x+4;
(2)∵y=x2±2$\sqrt{5}$x+4=(x±$\sqrt{5}$)2-1,
∴当x=$\sqrt{5}$或-$\sqrt{5}$时,二次函数的最小值为-1.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
18.方程x2-4x+4=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 有一个实数根 | D. | 没有实数根 |
15.一元二次方程x2-3x-7=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 有一个实数根 |
12.A、B两地相距80千米,一辆大汽车从A地开出2小时后,又从A地开出另一辆小汽车,已知小汽车的速度是大汽车速度的3倍,结果小汽车比大汽车早40分钟到达B地,求两种汽车每小时各走多少千米.设大汽车的速度为xkm/h,则下面所列方程正确的是( )
| A. | $\frac{80}{x}$-$\frac{80}{3x}$=40 | B. | $\frac{80}{x}$-$\frac{80}{3x}$=2.4 | C. | $\frac{80}{x}$-2=$\frac{80}{3x}$+$\frac{2}{3}$ | D. | $\frac{80}{x}$+2=$\frac{80}{3x}$-$\frac{2}{3}$ |
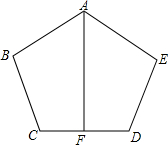 如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.
如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.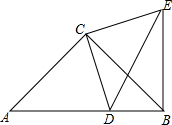 如图,AC=BC,∠CAB=∠CBA=45°,D为AB边上一个动点,CE=CD,∠CDE=∠CED=45°.
如图,AC=BC,∠CAB=∠CBA=45°,D为AB边上一个动点,CE=CD,∠CDE=∠CED=45°.