题目内容
17.在△ABC中,AB、BC、AC三边的长分别为$\sqrt{5}$、$\sqrt{10}$、$\sqrt{13}$,求这个三角形的面积.小芳同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点△ABC(即△ABC三个顶点都在小正方形的顶点处),如图1所示.这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你将△ABC的面积直接填写在横线上3.5.
思维拓展:
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC三边的长分别为$\sqrt{2}$a、$\sqrt{13}$a、$\sqrt{17}$a(a>0),请利用图2的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积填写在横线上6.5a2;
探索创新:
(3)请参照小芳的解答问题过程中的思想方法,证明:对于任意整数a,b,c,均有$\sqrt{{a^2}+{b^2}}+\sqrt{{b^2}+{c^2}}+\sqrt{{c^2}+{a^2}}≥\sqrt{2}$(a+b+c).
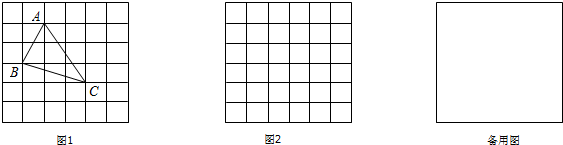
分析 (1)根据图形得出S△ABC=大矩形的面积-3个小三角形的面积,根据面积公式求出即可;
(2)先画出符合的三角形,再根据图形和面积公式求出即可;
(3)先画出图形,根据图形得到$\sqrt{{a}^{2}+{c}^{2}}$+$\sqrt{{b}^{2}+{c}^{2}}$+$\sqrt{{c}^{2}+{a}^{2}}$≥$\sqrt{2}$(a+b+c),依此即可证明.
解答 解:(1)△ABC的面积是4.5,理由是:
S△ABC=3×3-$\frac{1}{2}$×2×1-$\frac{1}{2}$×3×1-$\frac{1}{2}$×3×2
=9-1-1.5-3
=3.5.
故答案为:3.5;
(2)如图2的△ABC,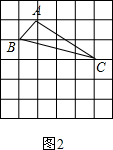
S△ABC=4a×3a-$\frac{1}{2}$×4a×a-$\frac{1}{2}$×3a×2a-$\frac{1}{2}$×a×a
=12a2-2a2-3a2-0.5a2
=6.5a2,
即△ABC的面积是6.5a2.
故答案为:6.5a2.
(3)证明:如图所示: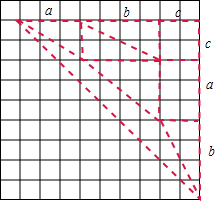
$\sqrt{{a}^{2}+{c}^{2}}$+$\sqrt{{b}^{2}+{c}^{2}}$+$\sqrt{{c}^{2}+{a}^{2}}$≥$\sqrt{2}$(a+b+c),a=b=c时等号成立.
点评 本题考查了勾股定理和三角形的面积公式的应用,解此题的关键是能正确画出格点三角形,难度较大.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
5.下面计算正确的是( )
| A. | 3+$\sqrt{3}$=3$\sqrt{3}$ | B. | $\sqrt{12}$÷$\sqrt{3}$=2 | C. | $\sqrt{2}$•$\sqrt{3}$=$\sqrt{5}$ | D. | $\sqrt{(-6)^{2}}$=-6 |
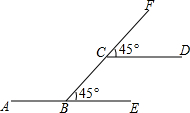 如图所示,一辆汽车在笔直的公路上行驶.第一次向左拐45°,再在笔直的公路上行驶一段距离后,第二次向右拐45°,请判断这辆汽车行驶的方向是否和原来的方向相同?为什么?
如图所示,一辆汽车在笔直的公路上行驶.第一次向左拐45°,再在笔直的公路上行驶一段距离后,第二次向右拐45°,请判断这辆汽车行驶的方向是否和原来的方向相同?为什么?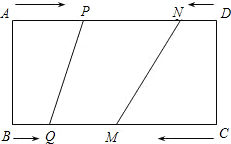 如图所示,在长方形ABCD中,BC=24cm,AB=10cm,点P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在长方形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.
如图所示,在长方形ABCD中,BC=24cm,AB=10cm,点P,Q,M,N分别从A,B,C,D出发沿AD,BC,CB,DA方向在长方形的边上同时运动,当有一个点先到达所在运动边的另一个端点时,运动即停止.已知在相同时间内,若BQ=xcm(x≠0),则AP=2xcm,CM=3xcm,DN=x2cm.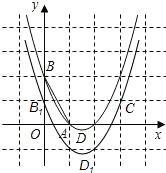 如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,所得抛物线与y轴的交点为B1,顶点为D1.若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,则点N的坐标为(1,-1),或(3,1).
如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,所得抛物线与y轴的交点为B1,顶点为D1.若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,则点N的坐标为(1,-1),或(3,1).