题目内容
16.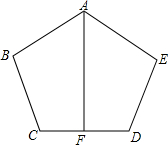 如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.
如图所示,已知AB=AE,∠ABC=∠AED,BC=ED,F是CD的中点,AF与CD有什么位置关系?说明理由.
分析 连接AC、AD,先由SAS证明△ABC≌△AED,得出对应边相等AC=AD,再由F是CD的中点,根据等腰三角形的三线合一性质即可得出结论.
解答 解:AF⊥CD,理由如下:
连接AC、AD,如图所示: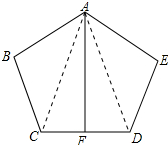 在△ABC和△AED中,
在△ABC和△AED中,
$\left\{\begin{array}{l}{AB=AE}&{\;}\\{∠ABC=∠AED}&{\;}\\{BC=ED}&{\;}\end{array}\right.$,
∴△ABC≌△AED(SAS),
∴AC=AD,
∵F是CD的中点,
∴AF⊥CD(三线合一).
点评 本题考查了全等三角形的判定与性质、等腰三角形的判定与性质;熟练掌握全等三角形的判定与性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
5.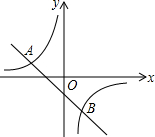 如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
 如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )
如图,一次函数y1=-x-1的图象与反比例函数y2=-$\frac{2}{x}$的图象交于A(-2,1),B(1,-2)两点,则使y2>y1的x的取值范围是( )| A. | -2<x<0或x>1 | B. | x<-2或x>1 | C. | x<-2或x>1 | D. | -2<x<1且x≠0 |
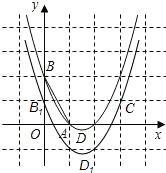 如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,所得抛物线与y轴的交点为B1,顶点为D1.若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,则点N的坐标为(1,-1),或(3,1).
如图,已知抛物线y=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,所得抛物线与y轴的交点为B1,顶点为D1.若点N在平移后的抛物线上,且满足△NBB1的面积是△NDD1面积的2倍,则点N的坐标为(1,-1),或(3,1).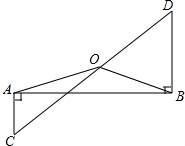 如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.
如图:AC⊥AB,DB⊥AB,OC=OD.求证:OA=OB.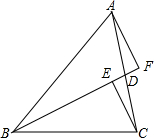 如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.
如图,BD是△ABC的中线,CE⊥BD于E,AF⊥BD交BD的延长线于F.请说明BE+BF=2BD.
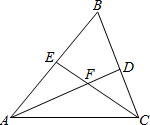 如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.
如图,在△ABC中,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.