题目内容
15.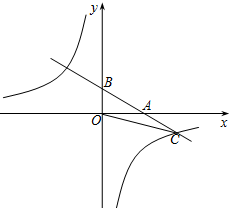 如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为2.
如图,直线y=ax+1(a≠0)与x轴交于点A,与y轴交于点B,与双曲线y=$\frac{k}{x}$在第四象限的交点为C.若点B与点C关于点A对称,且△BOC的面积为2.(1)求a、k的值;
(2)问:在x轴上是否存在这样的点P,使得△PBC为等腰三角形?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
分析 (1)先求出B点坐标,再由点B与点C关于点A对称得出AB=AC,根据△BOC的面积为2求出OA的长,故可得出A点坐标,进而得出C点坐标,代入反比例函数即可得出k的值;
(2)存在,分两种情况考虑:以O为圆心OA长为半径画弧,与x轴交于点P1,P2;以A为圆心,AO长为半径画弧,与x轴交于P3、P4点;分别求出坐标即可.
解答 解:(1)∵当x=0时,y=ax+1=1,
∴B(0,1).
∵点B与点C关于点A对称,
∴AB=AC.
∵△BOC的面积为2,
∴S△OAB=$\frac{1}{2}$S△BOC,即$\frac{1}{2}$×1×OA=1,解得OA=2,
∴A(2,0).
把A(2,0)代入直线y=ax+1得,2a+1=0,解得a=-$\frac{1}{2}$.
∵A(2,0),
∴点C的横坐标为4,
∴C点纵坐标为-1,
∴C(4,-1),
∴-1=$\frac{4}{x}$,解得k=-4.
(2)存在.
理由:∵B(0,1),C(4,-1),
∴BC=$\sqrt{(0-4)^{2}+(1+1)^{2}}$=$\sqrt{16+4}$=2$\sqrt{5}$.
①以B为圆心BC长为半径画弧,与x轴交于点P1,P2,
∴OP1=OP2=$\sqrt{{BP}^{2}-{OB}^{2}}$=$\sqrt{{(2\sqrt{5})}^{2}-{1}^{2}}$=$\sqrt{19}$,
∴P1(-$\sqrt{19}$,0),P2($\sqrt{19}$,0);
以C为圆心,BC长为半径画弧,与x轴交于P3、P4,
此时P3(4-$\sqrt{19}$,0),P4(4+$\sqrt{19}$,0);
综上,满足题意的P点坐标为P1(-$\sqrt{19}$,0),P2($\sqrt{19}$,0),P3(4-$\sqrt{19}$,0),P4(4+$\sqrt{19}$,0).
点评 此题考查的是反比例函数综合题,涉及到待定系数法求函数解析式,两函数交点坐标求法,等腰三角形的性质,以及坐标与图形性质,熟练掌握待定系数法是解本题的关键..

 初中学业考试导与练系列答案
初中学业考试导与练系列答案 如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )
如图,直线EF,GH被直线AB所截,直线AB交GH于点A,交EF于点B,已知∠EBA=60°,则下列说法中正确的是( )| A. | 若∠GAC=60°,则GH∥EF | B. | 若∠GAB=150°,则GH∥EF | ||
| C. | 若∠BAH=120°,则GH∥EF | D. | 若∠CAH=60°,则GH∥EF |
| A. | $\frac{2500}{x}$=$\frac{3000}{x-50}$ | B. | $\frac{2500}{x}$=$\frac{3000}{x+50}$ | C. | $\frac{2500}{x-50}$=$\frac{3000}{x}$ | D. | $\frac{2500}{x+50}$=$\frac{3000}{x}$ |
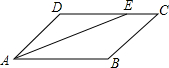 如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )
如图,在?ABCD中,AE平分∠BAD交边CD于点E.若AD=3,AB=4,则EC长为( )| A. | 3 | B. | 2 | C. | 1 | D. | 0.5 |
 解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$
解不等式组$\left\{\begin{array}{l}{\frac{1}{2}x>1}&{①}\\{1-x≥-3}&{②}\end{array}\right.$