题目内容
12.某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖包装纸盒(拼接处忽略不计),若有长方形纸板281张,正方形纸板122张,要做横式无盖、竖式无盖纸盒共80个.若设横式无盖纸盒为x个,则竖式无盖纸盒需80-x个.| 长方形纸板张数 | 正方形纸板张数 | |
| x个横式无盖共需要 | 3x | 2x |
| 80-x个竖式无盖共需要 | 4 | 80-x |
(2)请你设计生产方案,要求分别指明横式无盖纸盒和竖式无盖纸盒的生产个数;
(3)已知每个横式纸盒的利润为8元,每个竖式纸盒的利润为m元(m>0),
①请写出利润函数y关于x的函数关系式;
②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少?(用含m的代数式表示)
分析 (1)由题意即可得到结论;
(2)由生产横式的无盖长方体包装盒x个,则生产竖式的无盖长方体包装盒(50-x)个,根据题意可得两个关系式为:A种纸盒使用长方形纸板的个数+B种纸盒使用长方形纸板的个数≤长方形纸板的张数,A种纸盒使用正方形纸板的个数+B种纸盒使用正方形纸板的个数≤正方形纸板的张数,把相关数值代入求正整数解即可;
(3)①设销售利润为W元,生产横式纸盒x个,根据题意可得:总利润=横式纸盒的利润×横式纸盒的个数+竖式纸盒的利润×竖式纸盒的个数,即可得到结论;②再根据函数关系式确定x的值,即可得到答案.
解答 解:(1)如表中所示;
(2)∵生产横式的无盖长方体包装盒x个,则生产竖式的无盖长方体包装盒(80-x)个.
由题意得,$\left\{\begin{array}{l}{3x+4(80-x)≤281}\\{2x+80-x≤122}\end{array}\right.$,
解得,39≤x≤42.
∵x是整数,
∴x1=39,x2=40,x3=41,x4=42,
答:有4种生产方案,分别是:
生产横式包装盒39个,竖式包装盒41个;
生产横式包装盒40个,竖式包装盒40个;
生产横式包装盒41个,竖式包装盒39个;
生产横式包装盒42个,竖式包装盒38个;
(3)①设销售利润为W元,生产横式纸盒x个,
则w=8x+m(80-x)=(8-m)x+80m,
②当8-m<0,W随x 的增大而减小,
∴当x=39时,W最大,最大值为80m元;
当8-m>0,W随x 的增大而增大,
∴当x=42时,W最大,最大值为80m元.
点评 此题主要考查了一次函数的应用,一元一次方程的应用,将现实生活中的事件与数学思想联系起来,读懂题意,根据竖式及横式数量的关系设出未知数,列出不等式组求解是解题关键.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案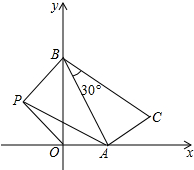 如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°;
如图,一次函数y=-$\sqrt{3}x+\sqrt{3}$的函数图象与x轴、y轴分别交于点A、B,以线段AB为直角边在第一象限内作Rt△ABC,使∠ABC=30°; 如图,对称轴为x=1的抛物线经过A(-1,0),B(4,5)两点.
如图,对称轴为x=1的抛物线经过A(-1,0),B(4,5)两点.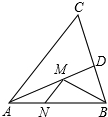 如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是$\sqrt{2}$.
如图,在锐角△ABC中,∠BAC=45°,AB=2,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是$\sqrt{2}$.