题目内容
7.商场销售某种衬衣,买入单价为40元,售出单价为60元.销售这种衬衣x件所获毛利润(售价-买入价)为y元.(1)求y关于x的函数表达式.
(2)若这种衬衣一年的销售量1000~1100间之间,则能或毛利润约多少元?
分析 (1)根据题意得即可得到结论;
(2)把销售量代入函数关系式即可得到结论.
解答 解:(1)根据题意得:y=(60-40)x=20x;
(2)当x=1000时,y=20000元,
当x=1100时,y=22000元,
∴能获毛利润约为:20000~22000之间.
点评 本题考查了一次函数的应用,掌握销售问题中的基本数量关系是解决问题的关键.

练习册系列答案
相关题目
5.某服装店进价为30元的内衣,以50元售出,平均每月能售出300件,经试销发现每件内衣每涨价10元,其月销售量就减少10件,为实现每月利润8700元,设定价为x元,则可得方程( )
| A. | 300(x-30)=8700 | B. | x(x-50)=8700 | ||
| C. | (x-30)[300-(x-50)]=8700 | D. | (x-30)(300-x)=8700 |
6.大于-1而小于$\sqrt{15}$的整数是( )
| A. | 0、1、2、3 | B. | 1、2、3 | C. | 2、3、4 | D. | 0、1、2、3、4 |
3.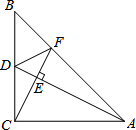 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖包装纸盒(拼接处忽略不计),若有长方形纸板281张,正方形纸板122张,要做横式无盖、竖式无盖纸盒共80个.若设横式无盖纸盒为x个,则竖式无盖纸盒需80-x个.
(1)把表格填写完整(用含x的代数式表示);
(2)请你设计生产方案,要求分别指明横式无盖纸盒和竖式无盖纸盒的生产个数;
(3)已知每个横式纸盒的利润为8元,每个竖式纸盒的利润为m元(m>0),
①请写出利润函数y关于x的函数关系式;
②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少?(用含m的代数式表示)
| 长方形纸板张数 | 正方形纸板张数 | |
| x个横式无盖共需要 | 3x | 2x |
| 80-x个竖式无盖共需要 | 4 | 80-x |
(2)请你设计生产方案,要求分别指明横式无盖纸盒和竖式无盖纸盒的生产个数;
(3)已知每个横式纸盒的利润为8元,每个竖式纸盒的利润为m元(m>0),
①请写出利润函数y关于x的函数关系式;
②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少?(用含m的代数式表示)
17.若(a+b)2加上一个单项式后等于(a-b)2,则这个单项式为( )
| A. | 2ab | B. | -2ab | C. | 4ab | D. | -4ab |
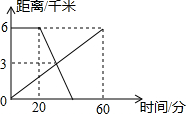 已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知:
已知A、B两地相距4千米,上午8:00,甲从A地出发步行到B地,8:20乙从B地出发骑自行车到A地,甲乙两人离A地的距离y(千米)与甲所用的时间X(分)之间的关系如图所示,由图中的信息可知: