题目内容
11.把下列各数填入相应的括号里:-7,0.$\stackrel{•}{6}$,$-\frac{3}{11}$,3.142,0,-2005,+|-6|,-(+7),-0.38整数有:-7,0,-2005,+|-6|,-(+7);负分数有$-\frac{3}{11}$,-0.38; 正有理数有0.$\stackrel{•}{6}$,3.142,+|-6|.
分析 根据形如-3,-2,-1,0,1,2,3是整数;小于零的分数是负分数,大于零的有理数是正有理数,可得答案.
解答 解:整数有:-7,0,-2005,+|-6|,-(+7);
负分数有:$-\frac{3}{11}$,-0.38;
正有理数有:0.$\stackrel{•}{6}$,3.142,+|-6|;
故答案为:-7,0,-2005,+|-6|,-(+7);$-\frac{3}{11}$,-0.38;0.$\stackrel{•}{6}$,3.142,+|-6|.
点评 本题考查了有理数,小于零的分数是负分数,大于零的有理数是正有理数,注意0既不是正数也不是负数.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
1.抛物线y=$\frac{1}{2}$x2向下平移一个单位得到抛物线( )
| A. | y=$\frac{1}{2}$(x+1)2 | B. | y=$\frac{1}{2}$(x-1)2 | C. | y=$\frac{1}{2}$x2+1 | D. | y=$\frac{1}{2}$x2-1 |
6.大于-1而小于$\sqrt{15}$的整数是( )
| A. | 0、1、2、3 | B. | 1、2、3 | C. | 2、3、4 | D. | 0、1、2、3、4 |
16.已知m是方程x2-2x-1=0的一个根,则代数式m2-2m的值等于( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
3.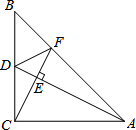 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
 已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )
已知,在△ABC中,AC=BC,∠ACB=90°,AD是中线,CE⊥AD交AB于点F,垂足为E,连接DF,则结论①∠BDF=∠ADC;②∠BFD=∠AFC;③CF+DF=AD.其中结论正确的个数是( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
12.某工厂用如图所示的长方形和正方形纸板做横式、竖式两种长方体形状的无盖包装纸盒(拼接处忽略不计),若有长方形纸板281张,正方形纸板122张,要做横式无盖、竖式无盖纸盒共80个.若设横式无盖纸盒为x个,则竖式无盖纸盒需80-x个.
(1)把表格填写完整(用含x的代数式表示);
(2)请你设计生产方案,要求分别指明横式无盖纸盒和竖式无盖纸盒的生产个数;
(3)已知每个横式纸盒的利润为8元,每个竖式纸盒的利润为m元(m>0),
①请写出利润函数y关于x的函数关系式;
②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少?(用含m的代数式表示)
| 长方形纸板张数 | 正方形纸板张数 | |
| x个横式无盖共需要 | 3x | 2x |
| 80-x个竖式无盖共需要 | 4 | 80-x |
(2)请你设计生产方案,要求分别指明横式无盖纸盒和竖式无盖纸盒的生产个数;
(3)已知每个横式纸盒的利润为8元,每个竖式纸盒的利润为m元(m>0),
①请写出利润函数y关于x的函数关系式;
②若仅从销售的利润考虑,以上哪种方案的利润最大?最大利润是多少?(用含m的代数式表示)