题目内容
1. 请你根据萌萌所给的如图所的内容,完成下列各小题.
请你根据萌萌所给的如图所的内容,完成下列各小题.(1)若m※n=1,m※2n=-2,分别求m和n的值;
(2)若m满足m※2≤0,且3m※(-8)>0,求m的取值范围.
分析 (1)根据题意列出关于m、n的方程组,求出m、n的值即可;
(2)根据题意列出关于m的不等式组,求出m的取值范围即可.
解答 解:(1)∵m※n=1,m※2n=-2,
∴$\left\{\begin{array}{l}{4m-3n=1}\\{4m-6n=-2}\end{array}\right.$,解得$\left\{\begin{array}{l}{n=1}\\{m=1}\end{array}\right.$;
(2)∵m※2≤0,3m※(-8)>0,
∴$\left\{\begin{array}{l}{4m-6≤0}\\{12m+24>0}\end{array}\right.$,解得-2<m≤$\frac{3}{2}$.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
19.下列算式中,运算结果为负数的是( )
| A. | -(-2)3 | B. | -|-1| | C. | -(-$\frac{5}{2}$) | D. | (-3)2 |
10.设n是自然数,则$\frac{{{{(-1)}^n}+{{(-1)}^{n+1}}}}{2}$的值为( )
| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
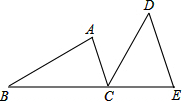 如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.