题目内容
10.设n是自然数,则$\frac{{{{(-1)}^n}+{{(-1)}^{n+1}}}}{2}$的值为( )| A. | 0 | B. | 1 | C. | -1 | D. | 1或-1 |
分析 根据题意目中的式子,分当n为偶数或者奇数两种情况进行计算,本题得以解决.
解答 解:当n为偶数时,
$\frac{{{{(-1)}^n}+{{(-1)}^{n+1}}}}{2}$=$\frac{1+(-1)}{2}=0$,
当n为奇数时,
$\frac{{{{(-1)}^n}+{{(-1)}^{n+1}}}}{2}$=$\frac{(-1)+1}{2}=0$,
故选A.
点评 本题考查有理数乘方,解答本题的关键是明确有理数乘方的计算方法,利用分类讨论的数学思想解答.

练习册系列答案
相关题目
19.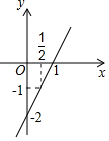 一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为( )
一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为( )
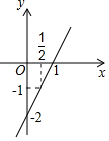 一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为( )
一次函数y=kx+b的图象如图所示,则关于x的方程kx+b=-1的解为( )| A. | x=0 | B. | x=1 | C. | x=$\frac{1}{2}$ | D. | x=-2 |
 请你根据萌萌所给的如图所的内容,完成下列各小题.
请你根据萌萌所给的如图所的内容,完成下列各小题.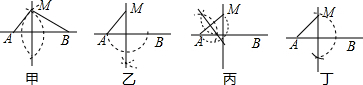
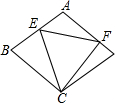 如图,E,F是菱形ABCD边AB与AD上的动点,在点E,F移动的过程中,保持AE=FD,若∠B=60°,AB=4,则△CEF的面积是否存在最小值?如果存在,求出这个值;如果不存在,请说明理由.
如图,E,F是菱形ABCD边AB与AD上的动点,在点E,F移动的过程中,保持AE=FD,若∠B=60°,AB=4,则△CEF的面积是否存在最小值?如果存在,求出这个值;如果不存在,请说明理由.