题目内容
附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:
正五边形α= ; 正六边形α= ; 正八边形α= ;
当正多边形的边数是n时,α= .
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:

正五边形α=
当正多边形的边数是n时,α=
考点:多边形内角与外角,等腰三角形的性质
专题:
分析:对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.通过分析找到各部分的变化规律后用一个统一的式子表示出变化规律是此类题目中的难点.
解答:解:∵五边形ABCDE是正五边形,
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BEA=∠ACB=
=36°,
∴∠CAE=108°-36°=72°,
∴α5=180°-∠EAO-∠AOE=72°;
同理:α6=60°,α8=45°,
当正多边形的边数是n时,α=
.
故答案为:72°; 60°; 45°;α=
.
∴AB=BC=AE,∠ABC=∠BAE=108°,
∴∠BEA=∠ACB=
| 180°-108° |
| 2 |
∴∠CAE=108°-36°=72°,
∴α5=180°-∠EAO-∠AOE=72°;
同理:α6=60°,α8=45°,
当正多边形的边数是n时,α=
| 360° |
| n |
故答案为:72°; 60°; 45°;α=
| 360° |
| n |
点评:本题主要考查了正多边形和圆的知识,学生通过特例分析从而归纳总结出一般结论的能力.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
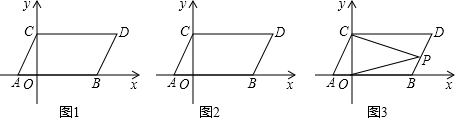
 如图,△ABC在直角坐标系中,
如图,△ABC在直角坐标系中,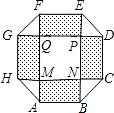 某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.
某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图所示),其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.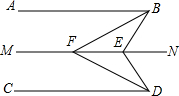 如图,直线AB∥MN∥CD,E,F为直线MN上的两点,BF平分∠ABE,DF平分∠CDE,∠BED=120°,求∠BFD的度数.
如图,直线AB∥MN∥CD,E,F为直线MN上的两点,BF平分∠ABE,DF平分∠CDE,∠BED=120°,求∠BFD的度数.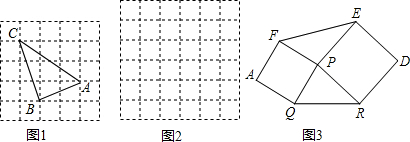
 如图,在平行四边形ABCD中,E为BC边上的一点,连接AE,BD且AE=AB.
如图,在平行四边形ABCD中,E为BC边上的一点,连接AE,BD且AE=AB.