题目内容
如图:在长方形ABCD中,∠B=90°点E在BC边上,过E作EF⊥AC于F,
(1)如图1:当BE=EC=3,AB=8时,求EF的长.
(2)如图2:若BG=EG,求证:AG=BG.
(3)如图3:若BG=EG=FG=BF,求:
的值.
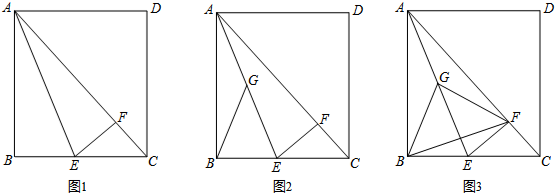
(1)如图1:当BE=EC=3,AB=8时,求EF的长.
(2)如图2:若BG=EG,求证:AG=BG.
(3)如图3:若BG=EG=FG=BF,求:
| AC |
| BC |

考点:四边形综合题,圆周角定理
专题:
分析:(1)求EF的长.EF为△AEC的高,所以我们可以利用相等,
AB•EC=
AC•EF通过其他边长,求得EF长度.
(2)证明AG=BG,只需得到∠GAB=∠GBA,已知中BG=EG,即可得出∠GBE=∠GEB,而在Rt△ABE中,∠GAB、∠GBA恰好为等角的余角.
(3)上一问中的条件在本问中又一次出现,所以上一问结论的本问使用的可能性较大,往往这是求解题目的突破口.那根据BG=EG=FG=BF和上问的AG=BG,可退得AG=BG=EG=FG=BF,可发现若G为圆心,ABEF四点都在圆上,且△BGF为等边三角形.∠BAF为
所对的圆周角,即∠BAC=
•60°=30°,此时
=
,结论显而易见.
| 1 |
| 2 |
| 1 |
| 2 |
(2)证明AG=BG,只需得到∠GAB=∠GBA,已知中BG=EG,即可得出∠GBE=∠GEB,而在Rt△ABE中,∠GAB、∠GBA恰好为等角的余角.
(3)上一问中的条件在本问中又一次出现,所以上一问结论的本问使用的可能性较大,往往这是求解题目的突破口.那根据BG=EG=FG=BF和上问的AG=BG,可退得AG=BG=EG=FG=BF,可发现若G为圆心,ABEF四点都在圆上,且△BGF为等边三角形.∠BAF为
 |
| BEF |
| 1 |
| 2 |
| AC |
| BC |
| 1 |
| sin∠BAC |
解答:(1)解:∵BE=EC=3
∴BC=6
在Rt△ABC中
∵AB=8
∴AC=10
∴S△AEC=
AB•EC=
•8•3=12
∵S△AEC=
AC•EF=
•10•EF
∴EF=2.4
(2)证明:∵GB=GE
∴∠GBE=GEB
在Rt△ABE中
∠BAG与∠GEB互余
∵∠ABE=90°
∴∠GBA与∠GBE互余
∴∠GAB=∠GBA
∴AG=BG
(3)解:∵BG=EG
∴AG=BG在Rt△ABC中
=sin∠BAC=sin30°=
∵BG=EG=FG=BF
∴AG=BG=EG=FG=EF
∴A、B、E、F四点共圆且△BGF为等边三角形
∴∠BGF=60°
∴∠BAF=
•∠BGF=30°
在Rt△ABC中
∵
=sin∠BAC=sin30°=
(如果没接触过三角函数,可以用“在含30°角的直角三角形中,30°所对的直角边等于斜边的一半”,也可以得出结论)
∴
=2
∴BC=6
在Rt△ABC中
∵AB=8
∴AC=10
∴S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
∵S△AEC=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF=2.4
(2)证明:∵GB=GE
∴∠GBE=GEB
在Rt△ABE中
∠BAG与∠GEB互余
∵∠ABE=90°
∴∠GBA与∠GBE互余
∴∠GAB=∠GBA
∴AG=BG
(3)解:∵BG=EG
∴AG=BG在Rt△ABC中
| BC |
| AC |
| 1 |
| 2 |
∵BG=EG=FG=BF
∴AG=BG=EG=FG=EF
∴A、B、E、F四点共圆且△BGF为等边三角形
∴∠BGF=60°
∴∠BAF=
| 1 |
| 2 |
在Rt△ABC中
∵
| BC |
| AC |
| 1 |
| 2 |
∴
| AC |
| BC |
点评:本题前两问难度不高,都属于基础题目.第三问相对技巧性较强,且图示不标准不容易得到思路.但是对于综合类题目,也有非常有效的做题技巧.一、多问时,注意如果本问题目中有“若…”的情况,一般来讲结论他问不能使用,但如果下问的“若…”包含前问的条件,这个时候解题往往要利用上文的结论.把精力放在这些点上,突破难题就容易的多.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
将二次函数y=2x2-8x-1化成y=a(x-h)2+k的形式,结果为( )
| A、y=2(x-2)2-1 |
| B、y=2(x-4)2+32 |
| C、y=2(x-2)2-9 |
| D、y=2(x-4)2-33 |
 如图,点B是半径为6的⊙O上一点,过点B作一个30°的圆周角∠ABC,则由弦AB、BC和
如图,点B是半径为6的⊙O上一点,过点B作一个30°的圆周角∠ABC,则由弦AB、BC和