题目内容
11.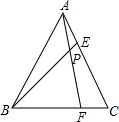 △ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.
△ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.(1)求证:△APE∽△ACF.
(2)若AE=1,求AP•AF的值.
(3)当P点处于线段BE什么位置时,△APE的面积等于四边形CFPE的面积?
分析 (1)由△ABC是等边三角形,得到∠C=60°,求得∠C=∠APE,根据相似三角形的判定定理得到△APE∽△ACF;
(2)根据相似三角形的性质得到$\frac{AE}{AF}=\frac{AP}{AC}$,代入数据得到AP•AF=3;
(3)根据三角形的外角的性质得到∠ABP=∠EAP,由△ABC是等边三角形,得到∠C=∠BAC=60°,AB=AC,根据全等三角形的性质得到S△APC=S△BEA,推出BP=EP,即可得到结论.
解答 解:(1)∵△ABC是等边三角形,
∴∠C=60°,
∵∠APE=60°,
∴∠C=∠APE,
∵∠PAE=∠CAF,
∴△APE∽△ACF;
(2)∵△APE∽△ACF,
∴$\frac{AE}{AF}=\frac{AP}{AC}$,
∵AC=3,AE=1,
∴AP•AF=3;
(3)∵∠APE=∠ABP+∠BAP=60°,∠BAP+EAP=60°,
∴∠ABP=∠EAP,
∵△ABC是等边三角形,
∴∠C=∠BAC=60°,AB=AC,
在△AFC与△BEA中,
$\left\{\begin{array}{l}{∠ABE=∠CAF}\\{AB=AC}\\{∠BAE=∠C}\end{array}\right.$,
∴△AFC≌△BEA,
∴S△APC=S△BEA,
∴S△ABP=S四边形CFPE,
若S△APE=S四边形CFPE,
则S△ABP=S△APE,
∴BP=EP,即P是BE的中点.
点评 本题考查了相似三角形的判定和性质,等边三角形的性质,全等三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
 如图,在正方形ABCD中,点O是对角线AC,BD的交点,点E在CD上,连接BE,过点C作CF⊥BE于点F,在BE上截取BG=CF,连接OF,OG.
如图,在正方形ABCD中,点O是对角线AC,BD的交点,点E在CD上,连接BE,过点C作CF⊥BE于点F,在BE上截取BG=CF,连接OF,OG.

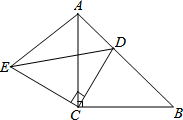 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.