题目内容
19.某中学开学初在商场购进A、B两种品牌的足球,购买A品牌足球花费了2500元,购买B品牌足球花费了2000元,且购买A品牌足球数量是购买B品牌足球数量的2倍,已知购买一个B品牌足球比购买一个A品牌足球多花30元.(1)求购买一个A品牌和一个B品牌的足球各需多少元.
(2)这所中学决定再次购进A,B两种品牌足球共50个,恰逢商场对两种品牌足球的售价进行调整,A品牌足球球售价比第一次购买时提高了8%,B品牌足球按第一次购买时售价的9折出售,如果这所中学此次购买A、B两种品牌足球的总费用不超过3260元,那么这所中学此次最多可购买多少个B品牌足球?
分析 (1)设购买一个A品牌足球需x元,购买一个B品牌足球需(x+30)元.接下来,依据购买A品牌足球数量是购买B品牌足球数量的2倍列方程求解即可;
(2)设此次可购买a个B品牌的足球,则购进A品牌足球(50-a)个,接下来依据总费用不超过3260元列不等式求解即可.
解答 解:(1)设购买一个A品牌足球需x元,购买一个B品牌足球需(x+30)元.
根据题意得:$\frac{2500}{x}$=$\frac{2000}{x+30}$×2.
解得:x=50.
经检验x=50是原方程的解.则x+30=80.
答:购买一个A品牌的足球需要50元,购买一个B品牌的足球需80元.
(2)设此次可购买a个B品牌的足球,则购进A品牌足球(50-a)个.
由题意得:50(1+8%)(50-a)+80×0.9a≤3260.
解得;a≤31$\frac{1}{9}$.
∵a是整数,
∴a最大可取31.
答:这所中学此次最多可购买31个B品牌的足球.
点评 本题主要考查的是分式方程的应用、一元一次不等式的应用,根据题意列出方程和不等式是解题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
10.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.
问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
| A. | $\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+2y=8}\\{2x+5y=10}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+2y=10}\\{x+5y=8}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=2}\\{2x+5y=8}\end{array}\right.$ |
4.下列各数中,最小的是( )
| A. | 0.02 | B. | 0.11 | C. | 0.1 | D. | 0.12 |
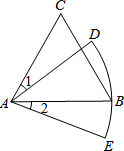 如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).
如图,△ABC是等边三角形,AC=9,以点A为圆心,AB长为半径画$\widehat{DE}$,若∠1=∠2,则$\widehat{DE}$的长为3π(结果保留π).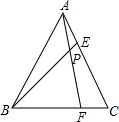 △ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.
△ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.