题目内容
20.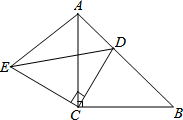 已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.
已知,如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,D为AB边上一点.(1)求证:△ACE≌△BCD;
(2)求证:2CD2=AD2+DB2.
分析 (1)本题要判定△ACE≌△BCD,已知△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,则DC=EA,AC=BC,∠ACB=∠ECD,又因为两角有一个公共的角∠ACD,所以∠BCD=∠ACE,根据SAS得出△ACE≌△BCD.
(2)由(1)的论证结果得出∠DAE=90°,AE=DB,从而求出AD2+DB2=DE2,即2CD2=AD2+DB2.
解答 证明:(1)∵△ABC和△ECD都是等腰直角三角形,
∴AC=BC,CD=CE,
∵∠ACB=∠DCE=90°,
∴∠ACE+∠ACD=∠BCD+∠ACD,
∴∠ACE=∠BCD,
在△ACE和△BCD中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACE=∠BCD}\\{CD=CE}\end{array}\right.$,
∴△AEC≌△BDC(SAS);
(2)∵△ACB是等腰直角三角形,
∴∠B=∠BAC=45度.
∵△ACE≌△BCD,
∴∠B=∠CAE=45°
∴∠DAE=∠CAE+∠BAC=45°+45°=90°,
∴AD2+AE2=DE2.
由(1)知AE=DB,
∴AD2+DB2=DE2,即2CD2=AD2+DB2.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及等角的余角相等的性质,熟记各性质是解题的关键.

练习册系列答案
 优百分课时互动系列答案
优百分课时互动系列答案
相关题目
10.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开方术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.
问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
问:牛、羊各直金几何?”
译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、
每只羊各值金多少两?”设每头牛值金x两,每只羊值金y两,可列方程组为( )
| A. | $\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{5x+2y=8}\\{2x+5y=10}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{5x+2y=10}\\{x+5y=8}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=2}\\{2x+5y=8}\end{array}\right.$ |
5.-$\sqrt{2}$的相反数是( )
| A. | -$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
12.若方程3x2-4x-4=0的两个实数根分别为x1,x2,则x1+x2=( )
| A. | -4 | B. | 3 | C. | $-\frac{4}{3}$ | D. | $\frac{4}{3}$ |
19.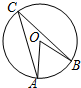 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
 如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )
如图,已知A,B,C在⊙O上,∠ACB=30°,则∠AOB等于( )| A. | 60° | B. | 50° | C. | 45° | D. | 30° |
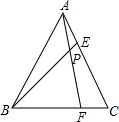 △ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.
△ABC是边长为3等边三角形,点E,点F分别在AC、BC边上,连结AF、BE相交于点P,∠APE=60°.
