题目内容
18.计算:(1)|$\frac{1}{100}$-$\frac{1}{99}$|+|$\frac{1}{101}$-$\frac{1}{100}$|-|$\frac{1}{101}$-$\frac{1}{99}$|
(2)|$\frac{1}{2}$-$\frac{1}{3}$|+|$\frac{1}{3}$-$\frac{1}{4}$|+|$\frac{1}{4}$-$\frac{1}{5}$|+…+|$\frac{1}{2014}$-$\frac{1}{2015}$|
分析 (1)、(2)先去绝对值符号,再根据有理数的加减法则进行计算即可.
解答 解:(1)原式=$\frac{1}{99}$-$\frac{1}{100}$+$\frac{1}{100}$-$\frac{1}{101}$-($\frac{1}{99}$-$\frac{1}{101}$)
=$\frac{1}{99}$-$\frac{1}{100}$+$\frac{1}{100}$-$\frac{1}{101}$-$\frac{1}{99}$+$\frac{1}{101}$
=0;
(2)原式=$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+$\frac{1}{4}$-$\frac{1}{5}$+…+$\frac{1}{2014}$-$\frac{1}{2015}$
=$\frac{1}{2}$-$\frac{1}{2015}$
=$\frac{2015-2}{4030}$
=$\frac{2013}{4030}$.
点评 本题考查的是有理数的加减混合运算,熟知绝对值的性质是解答此题的关键.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目
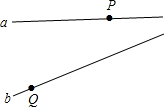 如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q
如图所示,直线a,b分别代表公路和河流,点P代表公路a上的公共汽车站,点Q