题目内容
10.(1)解不等式 $\frac{x-3}{2}$-1>$\frac{x-5}{3}$(2)解方程:x2+4x+3=0.
分析 (1)去分母,去括号,移项,合并同类项,系数化成1即可;
(2)求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)去分母得:3(x-3)-6>2(x-5),
3x-9-6>2x-10,
3x-2x>-10+9+6,
x>5;
(2)x2+4x+3=0,
△=42-4×1×3=4,
x=$\frac{-4±\sqrt{4}}{2}$,
x1=-1,x2=-3.
点评 本题考查了解一元一次不等式和解一元一次方程的应用,能灵活运用等式的性质和不等式的性质进行变形是解此题的关键.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
20.下列关系中,两个量之间为反比例函数关系的是( )
| A. | 正方形的面积S与边长a的关系 | |
| B. | 正方形的周长L与边长a的关系 | |
| C. | 长方形的长为a,宽为20,其面积S与a的关系 | |
| D. | 长方形的面积为40,长为a,宽为b,a与b的关系 |
20.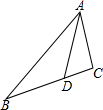 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
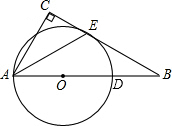 如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.
如图,Rt△ABC,∠C=90°,点D为AB上的一点,以AD为直径的⊙O与BC相切于点E,连接AE.