题目内容
20.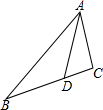 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=( )| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{9}{2}$ |
分析 过D作DP⊥AC交AC的延长线于P,DQ⊥AB于Q,根据角平分线的性质得到DP=DQ,根据S△ABD=$\frac{1}{2}$AB•DQ=$\frac{1}{2}$•DQ=3,求得DQ=1,得到DP=1,即可得到结论.
解答 解:过D作DP⊥AC交AC的延长线于P,DQ⊥AB于Q,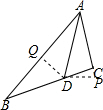
∵∠BAD=∠CAD,
∴DP=DQ,
∵S△ABD=$\frac{1}{2}$AB•DQ=$\frac{1}{2}$•DQ=3,
∴DQ=1,
∴DP=1,
∴S△ACD=$\frac{1}{2}$•AC•DP=$\frac{3}{2}$,
故选:C.
点评 本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
5.下列计算正确的是( )
| A. | a2+a2=a4 | B. | a3•a2=a6 | C. | (a2)3=a6 | D. | (a+b)2=a2+b2 |
9.-3的相反数是( )
| A. | -3 | B. | 3 | C. | $-\frac{1}{3}$ | D. | $\frac{1}{3}$ |
19.已知4n-m=4,则(m-4n)2-3(m-4n)-10的值是( )
| A. | -6 | B. | 6 | C. | 18 | D. | -38 |
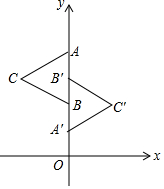 如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2).
如图,正三角形ABC与正三角形A′B′C′关于某点成中心对称,已知A、B′、B三点的坐标分别是(0,4)、(0,3)、(0,2). 太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,支撑角钢EF长为$\frac{{290\sqrt{3}}}{3}$cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为 30cm,点A到地面的垂直距离为50cm,则支撑角钢CD的长度是45cm,AB的长度是300cm.
太阳能光伏发电是一种清洁、安全、便利、高效的新兴能源,因而逐渐被推广使用.如图是太阳能电池板支撑架的截面图,其中的粗线表示支撑角钢,太阳能电池板与支撑角钢AB的长度相同,支撑角钢EF长为$\frac{{290\sqrt{3}}}{3}$cm,AB的倾斜角为30°,BE=CA=50cm,支撑角钢CD,EF与底座地基台面接触点分别为D,F,CD垂直于地面,FE⊥AB于点E.两个底座地基高度相同(即点D,F到地面的垂直距离相同),均为 30cm,点A到地面的垂直距离为50cm,则支撑角钢CD的长度是45cm,AB的长度是300cm.