题目内容
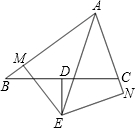 如图,已知BD=DC,BM=CN,ED⊥BC,EM⊥AB,EN⊥AC,垂足分别为D、M、N,请问AE是∠BAN的平分线吗,请说明理由.
如图,已知BD=DC,BM=CN,ED⊥BC,EM⊥AB,EN⊥AC,垂足分别为D、M、N,请问AE是∠BAN的平分线吗,请说明理由.考点:全等三角形的判定与性质,角平分线的性质,线段垂直平分线的性质
专题:计算题
分析:AE是∠BAN的平分线,理由为:连接BE,CE,由BD=DC,ED垂直于BC,得到BE=CE,再由BM=CN,利用HL得到直角三角形BEM与直角三角形ECN全等,利用全等三角形对应边相等得到EM=EN,再由EM垂直于AB,EC垂直于AN,利用角平分线逆定理判断即可得证.
解答: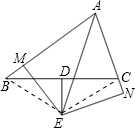 解:AE是∠BAN的平分线,理由为:
解:AE是∠BAN的平分线,理由为:
证明:连接BE、EC,
∵BD=CD,ED⊥BC,即ED是BC的垂直平分线,
∴BM=CE,
在Rt△BME和Rt△CNE中,
,
∴Rt△BME≌Rt△CNE(HL),
∴EM=EC,
∵EM⊥AB,EC⊥AN,
∴AE平分∠BAN.
 解:AE是∠BAN的平分线,理由为:
解:AE是∠BAN的平分线,理由为:证明:连接BE、EC,
∵BD=CD,ED⊥BC,即ED是BC的垂直平分线,
∴BM=CE,
在Rt△BME和Rt△CNE中,
|
∴Rt△BME≌Rt△CNE(HL),
∴EM=EC,
∵EM⊥AB,EC⊥AN,
∴AE平分∠BAN.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目