题目内容
已知：a=2-
，b=2+
，则a2b-ab2= ；
-2的整数部分是a，小数部分是b，
+2a= ．
| 3 |
| 3 |
| 19 |
| 3 |
| b |
考点：二次根式的化简求值,估算无理数的大小
专题：
分析：先把要求的式子进行变形，再把a，b的值代入进行计算即可；
根据题意先求出a，b的值，再代入要求的式子，然后进行计算即可．
根据题意先求出a，b的值，再代入要求的式子，然后进行计算即可．
解答：解：∵a=2-
，b=2+
，
∴a2b-ab2=ab（a-b）=（2-
）（2+
）（2-
-2-
）=-2
；
∵
-2的整数部分是a，
∴a=2，
∵
-2的小数部分是b，
∴b=
-4，
∴
+2a=
+2×2=
+4=
+4=
+8；
故答案为：-2
，
+8．
| 3 |
| 3 |
∴a2b-ab2=ab（a-b）=（2-
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
∵
| 19 |
∴a=2，
∵
| 19 |
∴b=
| 19 |
∴
| 3 |
| b |
| 3 | ||
|
| 3 | ||
|
3
| ||
| 3 |
| 19 |
故答案为：-2
| 3 |
| 19 |
点评：此题考查的是二次根式的化简求值及估算无理数大小的能力，解答此类题目的关键是先对无理数进行估算，再计算．
练习册系列答案
相关题目
如图，AB为的直径，点C在⊙O上，点P是直径AB上的一点（不与A，B重合），过点P作AB的垂线交BC的延长线于点Q．在线段PQ上取一点D，使DQ=DC，连接DC，试判断CD与⊙O的位置关系，并说明理由．
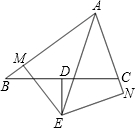如图，已知BD=DC，BM=CN，ED⊥BC，EM⊥AB，EN⊥AC，垂足分别为D、M、N，请问AE是∠BAN的平分线吗，请说明理由．
在△ABC中，分别以AB、AC为斜边作Rt△ABH、Rt△ACI，且使∠ABH=∠ACI=α，P为BC中点，则PH、PI的夹角为