题目内容
如图：四边形ABCD中，AB=CD，AD=BC，试回答下列问题：
（1）说明：∠A=∠C；
（2）若E、F分别在线段AB、CD上的一动点，且AE=CF，请你以F为一个端点，和图中已标明字母的某点连接成一条新线段，猜想并说明它与图中哪条已知线段相等（只需说明一组）
①我连结 ，并猜想 = ．
②理由： ．
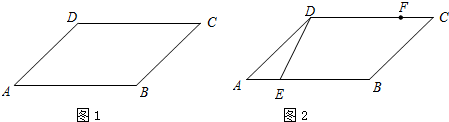
（1）说明：∠A=∠C；
（2）若E、F分别在线段AB、CD上的一动点，且AE=CF，请你以F为一个端点，和图中已标明字母的某点连接成一条新线段，猜想并说明它与图中哪条已知线段相等（只需说明一组）
①我连结
②理由：
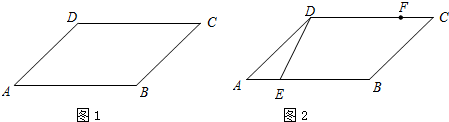
考点：全等三角形的判定与性质
专题：
分析：（1）两组对边相等的四边形是平行四边形，平行四边形的对角相等．
（2）平行四边形的对边相等，对角相等，可证明三角形全等．
（2）平行四边形的对边相等，对角相等，可证明三角形全等．
解答：解：（1）∵AB=CD，AD=BC，
∴四边形ABCD是平行四边形，
∴∠A=∠C．
（2）连接BF，并猜想DE=BF．
∵AE=CF，∠A=∠C，AD=BC，
在△ADE与△BCF中，
，
∴△ADE≌△BCF（SAS），
∴DE=BF．
∴四边形ABCD是平行四边形，
∴∠A=∠C．
（2）连接BF，并猜想DE=BF．
∵AE=CF，∠A=∠C，AD=BC，
在△ADE与△BCF中，
|
∴△ADE≌△BCF（SAS），
∴DE=BF．
点评：本题考查平行四边形的判定定理和性质定理，以及全等三角形的判定和性质．
练习册系列答案
相关题目
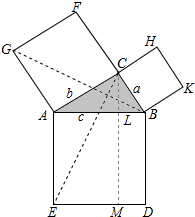关于勾股定理，有很多证法，在我国它们都是用拼图形面积方法来证明的．下面的证法是欧几里得证法．如图所示．在Rt△ABC的外侧，以各边为边长分别作正方形ABDE，BCHK，ACFG，它们的面积分别是c2，a2，b2．
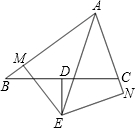如图，已知BD=DC，BM=CN，ED⊥BC，EM⊥AB，EN⊥AC，垂足分别为D、M、N，请问AE是∠BAN的平分线吗，请说明理由．