题目内容
19.双曲线y=$\frac{k}{x}$(k<0)与直线y=x+6相交于A、B两点.(1)当k=-5时,求AB的长;
(2)双曲线y=$\frac{k}{x}$(k<0)的同一支上有三点E(x1,y1)、F(x2,y2)、K($\frac{{x}_{1}+{x}_{2}}{2}$,y0).比较y0与$\frac{{x}_{1}+{x}_{2}}{2}$的大小.
分析 (1)解方程组得到A(-1,5),B(-5,1),根据两点间的距离公式即可得到结论;
(2)根据反比例函数的性质即可得到结论.
解答 解:(1)∵k=-5,
∴反比例函数的解析式为:y=$\frac{-5}{x}$,
解$\left\{\begin{array}{l}{y=-\frac{5}{x}}\\{y=x+6}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=5}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-5}\\{{y}_{2}=1}\end{array}\right.$,
∴A(-1,5),B(-5,1),
∴AB=$\sqrt{(-1+5)^{2}+(5-1)^{2}}$=4$\sqrt{2}$;
(2)当双曲线y=$\frac{k}{x}$(k<0)的三点E(x1,y1)、F(x2,y2)、K($\frac{{x}_{1}+{x}_{2}}{2}$,y0)在第二象限时,
∵y0>0,$\frac{{x}_{1}+{x}_{2}}{2}$<0,
∴y0>$\frac{{x}_{1}+{x}_{2}}{2}$;
当双曲线y=$\frac{k}{x}$(k<0)的三点E(x1,y1)、F(x2,y2)、K($\frac{{x}_{1}+{x}_{2}}{2}$,y0)在第四象限时,
∵y0<0,$\frac{{x}_{1}+{x}_{2}}{2}$>0,
∴y0<$\frac{{x}_{1}+{x}_{2}}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题,两点间的距离公式,反比例函数的性质,正确的求得交点坐标是解题的关键.

| A. | (-a3b)2=a6b2 | B. | 4a-2a=2 | C. | a6÷a3=a2 | D. | (a-b)2=a2-b2 |
| A. | x2+x2=2x4 | B. | x2•x3=x6 | C. | (a+1)2=a2+1 | D. | (-x)8÷x2=x6 |
| A. | $\sqrt{{a}^{2}+1}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
| A. | $\sqrt{16}$等于±4 | B. | -42的平方根是±4 | C. | 8的立方根是±2 | D. | -$\sqrt{5}$是5的平方根 |
 如图,下列条件中,能判定直线AB∥CD的是( )
如图,下列条件中,能判定直线AB∥CD的是( )| A. | ∠1=∠2 | B. | ∠1=∠3 | C. | ∠1+∠4=180° | D. | ∠2+∠4=180° |
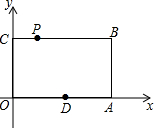 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).