题目内容
14.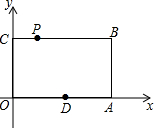 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(6,0)、(0,4),点P是线段BC上的动点,当△OPA是等腰三角形时,则P点的坐标是(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
分析 由矩形的性质得出BC=OA=6,AB=OC=4,∠B=∠OCB=90°,分三种情况:①当PO=PA时;②当AP=AO=6时;③当OP=OA=6时;分别求出PC的长,即可得出结果.
解答 解:∵四边形OABC是矩形,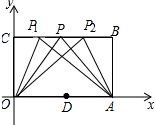
∴BC=OA=6,AB=OC=4,∠B=∠OCB=90°,
分三种情况:如图所示:
①当PO=PA时,P在OA的垂直平分线上,P是BC的中点,PC=3,
∴点P的坐标为(3,4);
②当AP=AO=6时,BP=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴PC=6-2$\sqrt{5}$,
∴P(6-2$\sqrt{5}$,4);
③当OP=OA=6时,PC=$\sqrt{{6}^{2}-{4}^{2}}$=2$\sqrt{5}$,
∴P(2$\sqrt{5}$,4).
综上所述:点P的坐标为(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
故答案为:(3,4)或(2$\sqrt{5}$,4)或(6-2$\sqrt{5}$,4).
点评 本题考查了矩形的性质、坐标与图形性质、等腰三角形的判定、勾股定理;熟练掌握矩形的性质,进行分类讨论是解决问题的关键.

练习册系列答案
相关题目
4.下列运算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | 3-2=-9 | C. | (a2)3=a6 | D. | 3a•2a=6a |
2.下列各组数中,不是勾股数的是( )
| A. | 5,12,13 | B. | 8,15,17 | C. | 3,4,5 | D. | 13,14,15 |
9.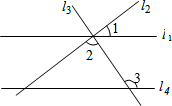 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
 如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )
如图,直线l1,l2,l3交于一点,直线l4∥l1,若∠3=124°,∠2=88°,则∠1的度数为( )| A. | 26° | B. | 36° | C. | 46° | D. | 56° |
6.在?ABCD中,若∠A+∠C=200°,则∠B的大小为( )
| A. | 160° | B. | 100° | C. | 80° | D. | 60° |
3.下列计算正确的是( )
| A. | a2+a3=a5 | B. | 2a(a+1)=2a2+2a | C. | (ab3)2=a2b5 | D. | (y-2x)(y+2x)=y2-2x2 |
 “瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )
“瓦当”是中国古代用以装饰美化建筑物檐头的建筑附件,其图案各式各样,属于中国特有的文化艺术遗产.下列“瓦当”的图案中,是轴对称图形的为( )


