题目内容
3. 如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.
如图,已知AB⊥BC,FC⊥BC,AB=BC,点E在BC上,AE⊥BF,垂足为G.求证:AE=BF.
分析 通过角的计算可得出∠A=∠FBC,结合AB=BC、∠ABE=∠BCF利用全等三角形的判定定理ASA,即可证出△ABE≌△BCF,再根据全等三角形的性质即可得出AE=BF.
解答 证明:∵AE⊥BF,AB⊥BC,
∴∠A+∠ABG=90°,∠ABG+∠FBC=90°,
∴∠A=∠FBC.
∵AB⊥BC,FC⊥BC,
∴∠ABE=∠BCF=90°.
在△ABE和△BCF中,$\left\{\begin{array}{l}{∠A=∠FBC}\\{AB=BC}\\{∠ABE=∠BCF}\end{array}\right.$,
∴△ABE≌△BCF(ASA),
∴AE=BF.
点评 本题考查了全等三角形的判定与性质,牢记各全等三角形的判定定理是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.
如图,AB是⊙O的直径,已知AB=2,C,D是⊙O的上的两点,且$\widehat{BC}$+$\widehat{BD}$=$\frac{2}{3}$$\widehat{AB}$,M是AB上一点,则MC+MD的最小值是$\sqrt{3}$.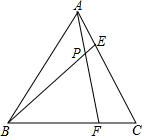 如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.
如图,在等边△ABC中,点F、E分别在BC、AC边上,AE=CF,AF与BE相交于点P.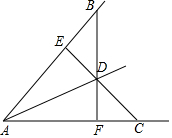 如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上.
如图,BD=CD,BF⊥AC于F,CE⊥AB于E.求证:点D在∠BAC的角平分线上.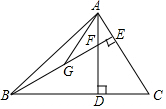 如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$.
如图,△ABC中,∠ABC=45°,高AD和BE交于F点,点G为BF的中点,AF=4,DF=6,则AG=$\frac{10\sqrt{170}}{17}$.