题目内容
14．在Rt△ABC，∠C=90°，如果b=8，a：c=3：5，则c=10．分析 根据题意画出图形，再根据勾股定理即可得出结论．
解答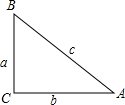 
解：如图所示，
∵a：c=3：5，
∴设a=3x，则c=5x．
∵在Rt△ABC，∠C=90°，b=8，
∴a2+b2=c2，即9x2+82=25x2，解得x=2，
∴c=5x=10．
故答案为：10．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
4．由$\frac{a}{b}$=$\frac{3}{5}$，不能推出的比例式是（ ）
| A． | $\frac{a}{3}$=$\frac{b}{5}$ | B． | $\frac{a+b}{b}$=$\frac{8}{5}$ | C． | $\frac{b-a}{a}$=$\frac{3}{2}$ | D． | $\frac{a+3}{b+5}$=$\frac{3}{5}$（b+5≠0） |
2．下列各式中，运算正确的是（ ）
| A． | a6÷a3=a2 | B． | $3\sqrt{\frac{a}{3}}=\sqrt{a}$ | C． | $2\sqrt{2}+3\sqrt{3}=5\sqrt{5}$ | D． | $\sqrt{6}÷\sqrt{3}=\sqrt{2}$ |