题目内容
4．若等腰直角三角形的外接圆半径的长为2，则其内切圆半径的长为（ ）| A． | 2$\sqrt{2}$-2 | B． | 2-$\sqrt{2}$ | C． | $\sqrt{2}$-1 | D． | $\sqrt{2}$ |
分析 由于直角三角形的外接圆半径是斜边的一半，由此可求得等腰直角三角形的斜边长，进而可求得两条直角边的长；然后根据直角三角形内切圆半径公式求出内切圆半径的长．
解答 解：∵等腰直角三角形外接圆半径为2，
∴此直角三角形的斜边长为4，两条直角边分别为2$\sqrt{2}$，
∴它的内切圆半径为：R=$\frac{1}{2}$（2$\sqrt{2}$+2$\sqrt{2}$-4）=2$\sqrt{2}$-2．
故选：A．
点评 本题考查了三角形的外接圆和三角形的内切圆，等腰直角三角形的性质，要注意直角三角形内切圆半径与外接圆半径的区别：直角三角形的内切圆半径：r=$\frac{1}{2}$（a+b-c）；（a、b为直角边，c为斜边）直角三角形的外接圆半径：R=$\frac{1}{2}$c．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14．下列运算中，错误的是（ ）
| A． | $\sqrt{3+5}$=$\sqrt{3}$+$\sqrt{5}$ | B． | $\sqrt{3×5}$=$\sqrt{3}$×$\sqrt{5}$ | C． | $\frac{\sqrt{24}}{\sqrt{6}}$=$\sqrt{\frac{24}{6}}$ | D． | （$\sqrt{2}$）3=2$\sqrt{2}$ |
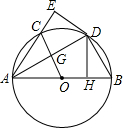如图，AB为⊙O的直径，点D在⊙O上，DH⊥AB于H，现将△AHD沿AD翻折得到△AED，AE交⊙O于点C，连接OC交AD于点G．
16．下列约分正确的是（ ）
| A． | $\frac{{a}^{6}}{{a}^{2}}$=a3 | B． | $\frac{a+x}{b+x}$=$\frac{a}{b}$ | C． | =a+b | D． | $\frac{-x-y}{x+y}$=-1 |