题目内容
 木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)
木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)考点:勾股定理的应用
专题:
分析:先根据等腰三角形的性质得出BD的长,在Rt△ABD中根据勾股定理求出AD的长即可.
解答:解:∵AB=CD=4,AD是△ABC的中线,BC=6,
∴AD⊥BC,BD=
BC=3.
由勾股定理,得AD=
=
=
m.
∵2<
,
∴长度为2m的木料不能做中柱AD.
∴AD⊥BC,BD=
| 1 |
| 2 |
由勾股定理,得AD=
| AB2-BD2 |
| 42-32 |
| 7 |
∵2<
| 7 |
∴长度为2m的木料不能做中柱AD.
点评:本题考查的是勾股定理的应用,在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法,关键是从题中抽象出勾股定理这一数学模型,画出准确的示意图.领会数形结合的思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若∠A与∠B互补,且∠A>∠B,则∠B的余角是( )
A、
| ||
B、
| ||
C、
| ||
D、∠A-
|
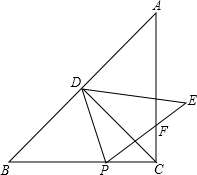 在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD
在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD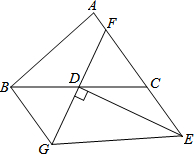 如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG.
如图,在△ABC中,已知D是BC边的中点,过点D的直线GF交AC于F,交AC的平行线BG于点G,DE⊥GF,交AC的延长线于点E,联结EG. 为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题:
为增强学生体质,各校要求学生每天在校参加体育锻炼的时间不少于1小时.我区为了解初三学生参加体育锻炼的情况,对部分初三学生进行了抽样调查,并将调查统计图表绘制如下.请你根据图表中信息解答下列问题: