题目内容
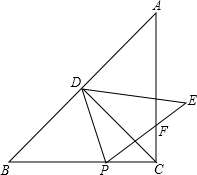 在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD
在Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,点P为BC边上一点,把△PBD沿PD翻折,点B落在点E处,设PE交AC于F,连接CD(1)求证:△PCF的周长=
| 2 |
(2)设DE交AC于G,若
| PE |
| EF |
| 5 |
| 3 |
考点:几何变换综合题
专题:
分析:(1)如图,连接CE.根据“直角三角形斜边上的中线等于斜边的一半”、等腰三角形的性质以及折叠的性质推知CP+PF+CF=BC=
CD;
(2)如图,作GK⊥EF于点K.设PF=5x,EF=CF=3x.在Rt△FCP中,利用勾股定理求得:CP=4x.根据(1)中的结论借助于方程求得x的值,从而得到CF=EF=3x=
.通过锐角三角函数的定义推知:
=
,故设GK=4a,FK=3a,EK=4a,结合已知条件求得a的值,则易知FG=5a.
| 2 |
(2)如图,作GK⊥EF于点K.设PF=5x,EF=CF=3x.在Rt△FCP中,利用勾股定理求得:CP=4x.根据(1)中的结论借助于方程求得x的值,从而得到CF=EF=3x=
| 3 |
| 2 |
| 2 |
| CP |
| CF |
| 4 |
| 3 |
解答: 解:(1)如图,连接CE.
解:(1)如图,连接CE.
∵Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,
∴BD=CD.
∵由翻折可知BD=DE,
∴CD=BD=DE,
∴∠DCE=∠DEC,
∴∠DCE-∠DEA=∠DEC-∠DEF,即∠FCE=∠FEC,
∴FC=FE,
∴CF+PF=PE=BP,
∴CP+PF+CF=BC=
CD
∴△PCF的周长=
CD;
(2)∵
=
,
∴设PF=5x,EF=CF=3x.
∵在Rt△FCP中,PF2=CP2+CF2,
∴CP=4x.
∵CP+PF+CF=
CD,
∴4x+5x+3x=6
,则x=
,CF=EF=3x=
如图,作GK⊥EF于点K.
∵tan∠GFE=tan∠PFC=
=
,
∴设GK=4a,FK=3a,EK=4a,
∴EF=7a=
,
∴a=
,FG=5a=
,
∴FG的长为
.
 解:(1)如图,连接CE.
解:(1)如图,连接CE.∵Rt△ABC中,∠ACB=90°,AC=BC,D为AB边的中点,
∴BD=CD.
∵由翻折可知BD=DE,
∴CD=BD=DE,
∴∠DCE=∠DEC,
∴∠DCE-∠DEA=∠DEC-∠DEF,即∠FCE=∠FEC,
∴FC=FE,
∴CF+PF=PE=BP,
∴CP+PF+CF=BC=
| 2 |
∴△PCF的周长=
| 2 |
(2)∵
| PF |
| EF |
| 5 |
| 3 |
∴设PF=5x,EF=CF=3x.
∵在Rt△FCP中,PF2=CP2+CF2,
∴CP=4x.
∵CP+PF+CF=
| 2 |
∴4x+5x+3x=6
| 2 |
| ||
| 2 |
| 3 |
| 2 |
| 2 |
如图,作GK⊥EF于点K.
∵tan∠GFE=tan∠PFC=
| 4x |
| 3x |
| 4 |
| 3 |
∴设GK=4a,FK=3a,EK=4a,
∴EF=7a=
| 3 |
| 2 |
| 2 |
∴a=
| 3 |
| 14 |
| 2 |
| 15 |
| 14 |
| 2 |
∴FG的长为
| 15 |
| 14 |
| 2 |
点评:本题考查了折叠的性质、勾股定理、直角三角形斜边上的中线以及锐角三角函数的定义等综合题型.需要学生具备一定的运算求解、推理论证的能力.

练习册系列答案
相关题目
如果分式
的值为0,则x的值是( )
| x2-4 |
| 3x+6 |
| A、2 | B、-2 | C、±2 | D、0 |
若三角形三边的长为下列各组数,则其中是直角三角形的是( )
| A、3,3,5 |
| B、4,5,6 |
| C、5,12,13 |
| D、5,5,6 |
 已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠DAC=∠FEB.
已知:如图,四边形ABCD中,AD∥BC,AC为对角线,点E在BC边上,点F在AB边上,且∠DAC=∠FEB.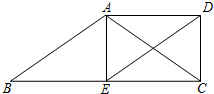 如图,在梯形ABCD中,AD∥BC,点E是BC的中点,连接AC,DE,AC=AB,DE∥AB.求证:四边形AECD是矩形.
如图,在梯形ABCD中,AD∥BC,点E是BC的中点,连接AC,DE,AC=AB,DE∥AB.求证:四边形AECD是矩形.
 木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)
木工师傅做一个人字形屋梁,如图,设计要求上弦AB=AC=4m,跨度BC为6m,现有一根木料打算做中柱AD(AD是△ABC的中线),判断长度为2m的木料能否做中柱AD,请通过计算说明.(注:设计只考虑长度、不计损耗)