Question

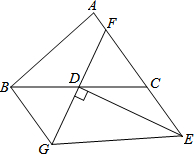如图，在△ABC中，已知D是BC边的中点，过点D的直线GF交AC于F，交AC的平行线BG于点G，DE⊥GF，交AC的延长线于点E，联结EG．
（1）说明BG与CF相等的理由．
（2）说明∠BGD与∠DGE相等的理由．

Answer 1

考点：全等三角形的判定与性质,线段垂直平分线的性质

专题：

分析：（1）求出BD=DC，∠GBD=∠DCF，证出△BDG≌△CDF即可；
（2）根据线段垂直平分线性质得出EF=EG，求出∠DFE=∠DGE，∠DFE=∠BGD，即可得出答案．

解答：解 （1）∵D为BC中点，
∴BD=DC（中点的定义），
∵BG∥FC（已知），
∴∠GBD=∠DCF（两直线平行，内错角相等），
在△BDG和△CDF中，

∠BDG=∠CDF(对顶角相等) BD=DC(已证) ∠GBD=∠DCF(已证)

，
∴△BDG≌△CDF（ASA），
∴BG=CF（全等三角形对应边相等）；

（2）∵DE为线段GF的中垂线（中垂线定义），
∴EF=EG（中垂线性质），
∴∠DFE=∠DGE（等边对等角），）
∵∠DFE=∠BGD（全等三角形对应角相等），
∴∠BGD=∠DGE（等量代换）．

点评：本题考查了全等三角形的性质和判定，线段垂直平分线性质，等腰三角形的性质的应用，主要考查学生的推理能力．