题目内容
10.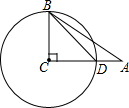 如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.
如图,在△ABC中,已知∠C=90°,sinA=$\frac{3}{5}$,以BC为半径的⊙C交AC边上一点D,若AD=4,求半径BC的长.
分析 设⊙C的半径为r,在Rt△ABC中,利用正弦的定义得到$\frac{r}{r+4}$=$\frac{4}{5}$,然后解方程求出r即可.
解答 解:设⊙C的半径为r,
在Rt△ABC中,∵sinA=$\frac{BC}{AC}$=$\frac{4}{5}$,
即$\frac{r}{r+4}$=$\frac{4}{5}$,解得r=16.
所以半径BC的长为16.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解直角三角形要用到的关系:锐角直角的关系:∠A+∠B=90°;三边之间的关系:a2+b2=c2;边角之间的关系:锐角三角函数关系.也考查了圆的认识.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.用加减消元法解方程组$\left\{\begin{array}{l}{4x+3y=2}\\{3x-4y=7}\end{array}\right.$时,有下列四种变形,其中正确的是( )
| A. | $\left\{\begin{array}{l}{12x+9y=2}\\{12x-16y=7}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{12x+3y=6}\\{12x-4y=28}\end{array}\right.$ | ||
| C. | $\left\{\begin{array}{l}{12x+9y=6}\\{12x-16y=28}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{16x+12y=2}\\{9x-12y=7}\end{array}\right.$ |
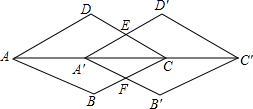 如图,将菱形ABCD沿AC方向平移至A′B′C′D′,A′D′交CD于点C,A′B′交BC于点F,判断A′FCE是不是菱形,并说明理由.
如图,将菱形ABCD沿AC方向平移至A′B′C′D′,A′D′交CD于点C,A′B′交BC于点F,判断A′FCE是不是菱形,并说明理由.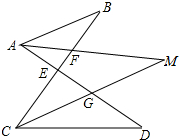 如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.
如图,AM是∠BAD的平分线,CM是∠BCD的平分线,AM、CM交于点M,CB、AM交于点F,AD、CM交于点G,AD、CB交于点E,∠B=32°,∠D=38°.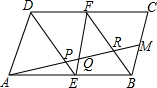 如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、EF.
如图,在?ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、EF.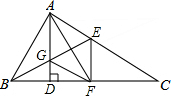 如图所示,在△ABC中,∠BAC=90°,AD⊥BC,BE,AF分别是∠ABC,∠DAC的平分线,BE和AD交于G,试说明四边形AGFE的形状.
如图所示,在△ABC中,∠BAC=90°,AD⊥BC,BE,AF分别是∠ABC,∠DAC的平分线,BE和AD交于G,试说明四边形AGFE的形状.