题目内容
10. 三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.
三棱柱的三视图如图所示,在△EFG中,FG=18cm,EG=14cm,∠EGF=30°,则AB的长为7cm.
分析 根据三视图的对应情况可得出,△EFG中FG上的高即为AB的长,进而求出即可.
解答  解:过点E作EQ⊥FG于点Q,
解:过点E作EQ⊥FG于点Q,
由题意可得出:EQ=AB,
∵EG=14cm,∠EGF=30°,
∴EQ=AB=$\frac{1}{2}$×14=7(cm).
故答案为:7.
点评 此题主要考查了由三视图解决实际问题,根据已知得出EQ=AB是解题关键.

练习册系列答案
相关题目
18.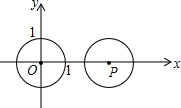 如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
 如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )| A. | 3 | B. | 1 | C. | 1,3 | D. | ±1,±3 |
15. 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
 如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )
如图,直线l1∥l2,∠2=65°,∠3=60°,则∠1为( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
19.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm或4$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm或4$\sqrt{3}$cm |
20.在已知实数-1,0,$\frac{1}{2}$,-$\sqrt{3}$,20150中,最小的一个实数是( )
| A. | -$\sqrt{3}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 0 |
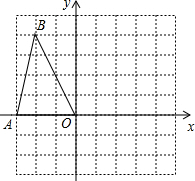 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2). 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.