题目内容
9.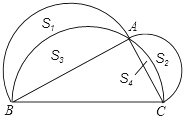 在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.
在△ABC中,∠C为锐角,分别以AB,AC为直径作半圆,过点B,A,C作$\widehat{BAC}$,如图,S1、S2、S3、S4分别表示图中四个“月牙形”的面积.若AB=4,AC=2,S1-S2=$\frac{π}{4}$,则S3-S4的值是$\frac{5}{4}$π.
分析 首先根据AB、AC的长求得S1+S3和S2+S4的值,然后两值相减即可求得结论.
解答 解:∵AB=4,AC=2,
∴S1+S3=2π,S2+S4=$\frac{1}{2}π$,
∵S1-S2=$\frac{π}{4}$,
∴(S1+S3)-(S2+S4)=(S1-S2)+(S3-S4)=$\frac{3}{2}$π,
∴S3-S4=$\frac{5}{4}$π.
故答案为$\frac{5}{4}$π.
点评 本题考查了整式的加减,圆的认识,解题的关键是正确的表示出S1+S3和S2+S4的值.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
18.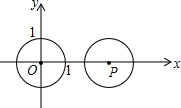 如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
 如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )
如图,平面直角坐标系中,⊙O半径长为1,点P在x轴上,⊙P的半径长为2,把⊙P向左平移,当⊙P与⊙O相切时,点P的横坐标的值为( )| A. | 3 | B. | 1 | C. | 1,3 | D. | ±1,±3 |
19.已知⊙O的直径CD=10cm,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8cm,则AC的长为( )
| A. | 2$\sqrt{5}$cm | B. | 4$\sqrt{5}$cm | C. | 2$\sqrt{5}$cm或4$\sqrt{5}$cm | D. | 2$\sqrt{3}$cm或4$\sqrt{3}$cm |
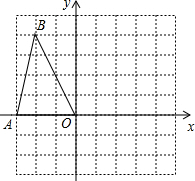 如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).
如图,正方形网格中的每一个小正方形的边长都是1,△AOB的三个顶点都在格点上,以O为坐标原点,建立如图平面直角坐标系,若把△AOB绕着点O顺时针旋转90°,得到△A1OB1,则点B旋转后的对应点B1的坐标为(4,2).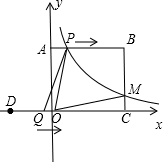 如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒.
如图,平面直角坐标系(单位:cm)中,B(5,4),D(-3,0),过B作BC⊥x轴于C,BA⊥y轴于A,点P从点A出发,以每秒1cm的速度沿A→B方向向终点B运动;点Q从点D出发,以每秒2cm的速度沿D→C方向向终点C运动,已知动点P、Q同时出发,当点P,点Q有一点到达终点时,P、Q都停止运动,设运动时间为t秒. 如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.
如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长(小于AB的长)为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D.