题目内容
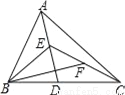
如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )
A. 2 cm2 B. 1 cm2 C. 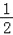 cm2 D.
cm2 D. 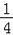 cm2
cm2
练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
题目内容
如图,在△ABC中,已知点D、E、F分别是边BC、AD、CE上的中点,且S△ABC=4cm2,则S△BEF的值为( )

A. 2 cm2 B. 1 cm2 C. 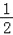 cm2 D.
cm2 D. 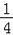 cm2
cm2
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案