题目内容
13．计算：（1）${（\sqrt{2011}-2011）^0}-{（-\frac{1}{2010}）^{-1}}$+sin60°×tan30°
（2）先化简，再求值：$\frac{{{a^2}-4}}{{{a^2}+6a+9}}÷\frac{a-2}{2a+6}$，其中a=-5．
分析 （1）原式第一项利用零指数幂法则计算，第二项利用负指数幂法则计算，最后一项利用特殊角的三角函数值计算即可得到结果；
（2）原式利用除法法则变形，约分得到最简结果，把a的值代入计算即可求出值．
解答 解：（1）原式=1-（-2010）+$\frac{\sqrt{3}}{2}$×$\frac{\sqrt{3}}{3}$=1+2010+$\frac{1}{2}$=2011$\frac{1}{2}$；
（2）原式=$\frac{（a+2）（a-2）}{（a+3）^{2}}$•$\frac{2（a+3）}{a-2}$=$\frac{2（a+2）}{a+3}$，
当a=-5时，原式=$\frac{2×（-5+2）}{-5+3}$=3．
点评 此题考查了分式的化简求值，以及实数的运算，熟练掌握运算法则是解本题的关键．
练习册系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
3．下列计算中，正确的是（ ）
| A． | $\sqrt{4}=2$ | B． | $\root{3}{9}=3$ | C． | $\root{3}{8}=±2$ | D． | $\sqrt{{{（-3）}^2}}=±3$ |
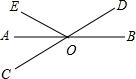如图，已知直线AB、CD相交于O点，OA平分∠EOC，∠EOC=60°，则∠BOD=30°．