题目内容
10.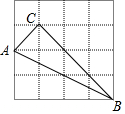 如图,在4×4的方格纸中,每个小方格的边长都是1,△ABC的三个顶点分别在方格的格点上.
如图,在4×4的方格纸中,每个小方格的边长都是1,△ABC的三个顶点分别在方格的格点上.(1)求△ABC的面积;
(2)求AB边上的高.
分析 (1)由矩形的面积减去三个直角三角形的面积即可;
(2)由勾股定理和勾股定理的逆定理证出△ABC是直角三角形,再由三角形面积关系即可得出结果.
解答 解:(1)△ABC的面积=3×4-$\frac{1}{2}$×4×2-$\frac{1}{2}$×3×3-$\frac{1}{2}$×1×1=3;
(2)∵AC2=12+12=2,BC2=32+32=18,AB2=22+42=20,
∴AC2+BC2=AB2,
∴△ABC是直角三角形,∠ACB=90°,
∴AB边上的高=$\frac{AC•BC}{AB}$=$\frac{\sqrt{2}×3\sqrt{2}}{2\sqrt{5}}$=$\frac{3\sqrt{5}}{5}$.
点评 此题考查了勾股定理与勾股定理的逆定理.此题比较简单,解题的关键是掌握勾股定理与勾股定理的逆定理的应用,掌握数形结合思想的应用.

练习册系列答案
相关题目
20. 如图中几何体的主视图是( )
如图中几何体的主视图是( )
 如图中几何体的主视图是( )
如图中几何体的主视图是( )| A. |  | B. |  | C. |  | D. |  |
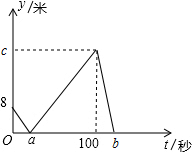 甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.
甲、乙两人在直线跑道上同起点同终点同方向匀速跑步500米,先到终点的人原地休息.已知甲先出发2s,在跑步过程中,甲、乙两人的距离y(m)与乙出发的时间t(s)之间的关系如图所示,给出的下结论:①a=8,②c=92,③b=123,其中正确的是①②③.