题目内容
12. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3(1)求OE长.
(2)判断四边形ADOC的形状.
分析 (1)连接OC,设OA=OB=OC=2x,求出AE=x,BE=2x,OE=2x-x=x,根据垂径定理求出CE=DE=3,根据勾股定理得出方程,求出方程的解即可;
(2)先求出四边形是平行四边形,再根据菱形的判定得出即可.
解答 解:(1)连接OC,
设OA=OB=OC=2x,
∵AE:BE=1:3,
∴AE=x,BE=2x,OE=2x-x=x,
∵弦CD⊥AB于点E,CD=6,
∴CE=DE=$\frac{1}{2}$CD=3,∠CEO=90°
在Rt△CEO中,由勾股定理得:OE2+CE2=OC2,
x2+32=(2x)2,
x=$\sqrt{3}$(负数舍去),
∴0E=$\sqrt{3}$;
(2)四边形ADOC的形状是菱形,
理由是:
∵CE=DE,AE=OE=x=$\sqrt{3}$,
∴四边形ADOC是平行四边形,
∵OC=OD,
∴四边形ADOC是菱形.
点评 本题考查了平行四边形的判定,菱形的判定,垂径定理,勾股定理的应用,能灵活运用定理进行推理和计算是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.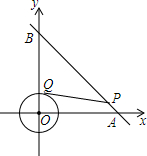 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
 如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )
如图,⊙O是以原点为圆心,2为半径的圆,点P是直线y=-x+4上的一点,过点P作⊙O的一条切线PQ,Q为切点,则切线长PQ的最小值为( )| A. | 3 | B. | 2 | C. | 3-$\sqrt{2}$ | D. | 2 $\sqrt{2}$ |
 如图∠ABC=∠CDB=90°,AC∥BD.
如图∠ABC=∠CDB=90°,AC∥BD.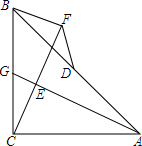 等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF.
等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF. 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使点A落在四边形对角线BD上的点G处,EG的延长线交直线BC于点F.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使点A落在四边形对角线BD上的点G处,EG的延长线交直线BC于点F.