题目内容
20.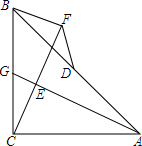 等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF.
等腰Rt△ABC中,∠ACB=90°,AC=BC,点G是BC上一点,CF⊥AG于E,BF⊥CF,D为AB中点,连接DF.(1)求证:△AEC≌△CFB;
(2)求证:EF=$\sqrt{2}$DF.
分析 (1)根据垂直的定义得到∠BCF=∠CAE=90°-∠ACE,根据全等三角形的判定即可得到结论;
(2)连接CD,DE,根据等腰直角三角形的性质得到CD=BD,∠CDB=90°,根据余角的性质得到∠FBD=∠DCE,由全等三角形的性质得到AE=CF,CE=BF,推出△BFD≌△CDE,由全等三角形的性质得到DF=DE,∠FDB=∠EDC,证得△DEF是等腰直角三角形,即可得到结论.
解答 证明:(1)∵CF⊥AG,BC⊥CF,
∴∠BCF=∠CAE=90°-∠ACE
在△AEC≌△CFB,
$\left\{\begin{array}{l}{AC=BC}\\{∠BCF=∠CAE}\\{∠CEA=∠CFB=90°}\end{array}\right.$,
∴△AEC≌△CFB;
(2)连接CD,DE,
∵等腰Rt△ABC中,∠ACB=90°,AC=BC,
∴CD=BD,∠CDB=90°,
∵∠CDB=∠CFB=90°,
∴∠FBD=∠DCE,
∵△AEC≌△CFB,
∴AE=CF,CE=BF,
在△BFD与△CDE中,
$\left\{\begin{array}{l}{BF=CE}\\{∠FBD=∠ECD}\\{BD=CD}\end{array}\right.$,
∴△BFD≌△CDE,
∴DF=DE,∠FDB=∠EDC,
∴∠EDC+∠EDB+∠BDF+∠BDE=90°,
∴△DEF是等腰直角三角形,
∴EF=$\sqrt{2}$DF.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.

练习册系列答案
相关题目
11.生活与数学
(1)小明同学在某月的日历上圈出2×2个数,正方形的方框内的四个数的和是32,那么这四个数是4,5,11,12.
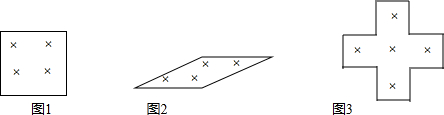
(2)小亮也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是7,8,13,14.
(3)小红也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是10.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号.
| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |

(2)小亮也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是7,8,13,14.
(3)小红也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是10.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号.
15.为了比较甲、乙两名射击运动员的射击成绩谁更稳定,每人各射击10次,并对这10次成绩(环)进行统计,如果两人的平均成绩相等,甲、乙的方差分别是0.3、0.5,则下列说法正确的是( )
| A. | 甲的射击成绩更稳定 | B. | 乙的射击成绩更稳定 | ||
| C. | 甲、乙的射击成绩一样稳定 | D. | 无法确定甲、乙射击成绩谁更稳定 |
 如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.
如图,CD是Rt△ABC的斜边AB上的高,E是BC上任意一点,EF⊥AB于点F.求证:AC2=AD•AF+CD•EF.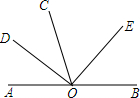 如图,O是直线AB上的点,OD是∠AOC的平分线,∠COD=28°,∠DOE=90°.
如图,O是直线AB上的点,OD是∠AOC的平分线,∠COD=28°,∠DOE=90°. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3