题目内容
17. 已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使点A落在四边形对角线BD上的点G处,EG的延长线交直线BC于点F.
已知:如图,在四边形ABCD中,AD∥BC,∠ABC=90°.点E为边AD上一点,将△ABE沿直线BE折叠,使点A落在四边形对角线BD上的点G处,EG的延长线交直线BC于点F.(1)点E可以是AD的中点吗?请说明理由;
(2)求证:△ABG∽△BFE;
(3)设AD=a,AB=b,BC=c.当四边形EFCD为平行四边形时,求a,b,c应满足的关系.
分析 (1)根据题意得出AE=GE,∠EGB=∠EAB=90°,在Rt△EGD中,GE<ED,因此AE<ED,即可得出结论;
(2)由平行线的性质得出∠AEB=∠EBF,再由折叠的性质得出∠EBF=∠BEF,证出FE=FB,△FEB为等腰三角形,证出∠ABG=∠EFB,由等腰三角形的性质和三角形内角和定理得出∠BAG=∠FBE,即可得出结论;
(3)过点D作DH⊥BC,由平行四边形的性质得出∠C=∠EFB,由相似三角形的性质得出∠EFB=∠GBA,因此∠C=∠GBA,证明△ABD∽△HCD,得出对应边成比例,即可得出结论.
解答 (1)解:点E不可以是AD的中点;理由如下:
根据题意得:AE=GE,∠EGB=∠EAB=90°,
∴Rt△EGD中,GE<ED,
∴AE<ED,
因此点E不可以是AD的中点.
(2)证明:∵AD∥BC,
∴∠AEB=∠EBF
∵△ABE沿直线BE折叠,
∴△EAB≌△EGB,
∴∠AEB=∠BEG,
∴∠EBF=∠BEF,∴FE=FB,
∴△FEB为等腰三角形.
∵∠ABG+∠GBF=90°,∠EFB+∠GBF=90°,
∴∠ABG=∠EFB,
在等腰△ABG和△FEB中,
∠BAG=$\frac{1}{2}$(180°-∠ABG),∠FBE=$\frac{1}{2}$(180°-∠EFB),
∴∠BAG=∠FBE,
∴△ABG∽△BFE.
(3)解:a2+b2=ac.理由如下:
过点D作DH⊥BC,如图所示:
∵四边形EFCD为平行四边形,
∴EF∥DC,
∴∠C=∠EFB,
∵△ABG∽△BFE,
∴∠EFB=∠GBA,
∴∠C=∠GBA,
∵∠DAB=∠DHC=90°,
∴△ABD∽△HCD,
∴$\frac{AD}{DH}=\frac{AB}{HC}$,
∴$\frac{a}{b}=\frac{b}{c-a}$,
∴a2+b2=ac.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、折叠的性质、全等三角形的性质、等腰三角形的判定与性质、三角形内角和定理、平行四边形的性质等知识;本题综合性强,有一定难度,证明三角形相似是解决问题的关键.

 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | SSS | B. | SAS | C. | SSA | D. | ASA |
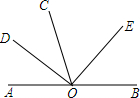 如图,O是直线AB上的点,OD是∠AOC的平分线,∠COD=28°,∠DOE=90°.
如图,O是直线AB上的点,OD是∠AOC的平分线,∠COD=28°,∠DOE=90°. 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3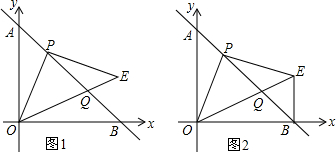
 如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOC=76°,则∠BOM=142°.
如图,直线AB,CD交于点O,射线OM平分∠AOC,若∠AOC=76°,则∠BOM=142°.