题目内容
1.在Rt△ABC中,a、b、c分别为∠A、∠B、∠C的对边,∠C=90°,根据下列已知条件,求这个三角形未知的边和角.(要求画出符合题意的图形)(1)b=2$\sqrt{3}$,c=4
(2)c=8,∠A=60°
(3)b=7,∠A=45°
(4)a=24,b=8$\sqrt{3}$.
分析 (1)先利用勾股定理计算出a,再利用正弦的定义求出∠A的度数,然后利用互余求∠B的度数;
(2)先利用互余求∠B的度数,再利用∠B的正弦求出b,然后利用勾股定理计算出c的值;
(3)先利用互余求∠B的度数,再利用等腰三角形的性质得到a=b=7,然后利用勾股定理计算出c的值;
(4)先利用计算∠A的正切值,这样可求出∠A的度数,再利用互余求∠B的度数,然后利用∠B的正弦求c的值.
解答 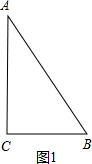 解:(1)如图1,
解:(1)如图1,
a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{{4}^{2}-(2\sqrt{3})^{2}}$=2,
∵sinA=$\frac{a}{c}$=$\frac{2}{4}$=$\frac{1}{2}$,
∴∠A=30°,
∴∠B=90°-∠A=60°;
(2)如图2,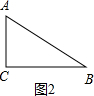 ∠B=90°-∠A=90°-60°=30°;
∠B=90°-∠A=90°-60°=30°;
∵sinB=sin30°=$\frac{b}{c}$=$\frac{1}{2}$,
∴b=$\frac{1}{2}$×8=4,
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{{8}^{2}-{4}^{2}}$=4$\sqrt{3}$;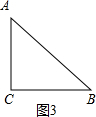 (3)如图3,
(3)如图3,
∠B=90°-∠A=90°-45°=45°,
∴a=b=7,
∴c=$\sqrt{{7}^{2}+{7}^{2}}$=7$\sqrt{2}$;
(4)如图4,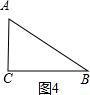 ∵tanA=$\frac{a}{b}$=$\frac{24}{8\sqrt{3}}$=$\sqrt{3}$,
∵tanA=$\frac{a}{b}$=$\frac{24}{8\sqrt{3}}$=$\sqrt{3}$,
∴∠A=60°,
∴∠B=90°-∠A=90°-60°=30°;
∴c=$\frac{b}{sinB}$=$\frac{8\sqrt{3}}{sin30°}$=16$\sqrt{3}$.
点评 本题考查了解直角三角形:在直角三角形中,由已知元素求未知元素的过程就是解直角三角形.解决本题的关键是灵活应用勾股定理和锐角三角函数的定义.

| 日 | 一 | 二 | 三 | 四 | 五 | 六 |
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
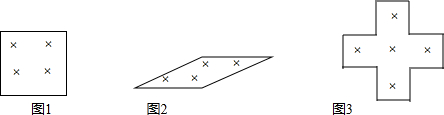
(2)小亮也在上面的日历上圈出2×2个数,斜框内的四个数的和是42,则它们分别是7,8,13,14.
(3)小红也在日历上圈出5个数,呈十字框形,它们的和是50,则中间的数是10.
(4)某月有5个星期日的和是75,则这个月中最后一个星期日是29号.
 如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3
如图,AB为⊙O的直径,弦CD⊥AB于点E,若CD=6,且AE:BE=1:3
 如图,OA表示北偏东32°的方向,则OB表示南偏东43°的方向.
如图,OA表示北偏东32°的方向,则OB表示南偏东43°的方向.