题目内容
用一张半径为10厘米的圆形纸板裁一个面积最大的正八边形,求八边形的面积.
考点:正多边形和圆
专题:
分析:根据题意画出图形,由正八边形的特点求出∠AOB的度数,过点B作BD⊥OA于点D,根据勾股定理求出BD的长,由三角形的面积公式求出△AOB的面积,进而可得出结论.
解答: 解:如图所示,
解:如图所示,
∵AB是正八边形的一条边,
∴∠AOB=
=45°.
过点B作BD⊥OA于点D,设BD=x,则2BD2=OB2,即2x2=102,解得x=5
,
∴S△AOB=
OA•BD=
×10×5
=25
,
∴S正八边形=8S△AOB=8×25
=200
.
 解:如图所示,
解:如图所示,∵AB是正八边形的一条边,
∴∠AOB=
| 360° |
| 8 |
过点B作BD⊥OA于点D,设BD=x,则2BD2=OB2,即2x2=102,解得x=5
| 2 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
∴S正八边形=8S△AOB=8×25
| 2 |
| 2 |
点评:本题考查的是正多边形和圆,根据题意画出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 a,b两数在数轴上的位置如图,下列结论正确的是( )
a,b两数在数轴上的位置如图,下列结论正确的是( )| A、a>0,b<0 |
| B、a<0,b>0 |
| C、ab>0 |
| D、以上都不对 |
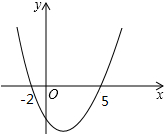 已知二次函数y=ax2-4x+c的图象如图所示.
已知二次函数y=ax2-4x+c的图象如图所示.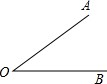 如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.
如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.