题目内容
 如图,直线y=
如图,直线y=| 1 |
| 3 |
| k |
| x |
| 5 |
| 2 |
A、
| ||
| B、1 | ||
| C、2 | ||
D、
|
考点:反比例函数与一次函数的交点问题
专题:
分析:把y=-1代入一次函数的解析式,即可求得横坐标,即△OCD中,CD边上的高,然后求得D的坐标,利用待定系数法求得反比例函数的解析式.
解答:解:在y=
x-2中令y=-1,得
x-2=-1,解得:x=3,
∵S△OCD=
CD×3=
,
∴CD=
,
则D的纵坐标是:
-1=
,
∴D的坐标是(3,
),
把D(3,
)代入y=
得:k=2.
故选C.
| 1 |
| 3 |
| 1 |
| 3 |
∵S△OCD=
| 1 |
| 2 |
| 5 |
| 2 |
∴CD=
| 5 |
| 3 |
则D的纵坐标是:
| 5 |
| 3 |
| 2 |
| 3 |
∴D的坐标是(3,
| 2 |
| 3 |
把D(3,
| 2 |
| 3 |
| k |
| x |
故选C.
点评:本题考查了待定系数法求函数的解析式,正确求得D的坐标是关键.

练习册系列答案
相关题目
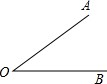 如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.
如图,A、B两点在∠O的两边上,满足OA=OB,用直尺和圆规作出∠O的平分线与OB的垂直平分线,两线相交于点P(不写作法,保留作图痕迹).试问:点P是否在OA的垂直平分线?猜想PA、PB之间的数量关系并说明理由.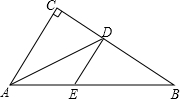 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE∥CA,CD=12,BD=15,求线段AE、BE的长.