题目内容
14.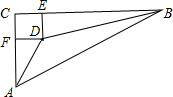 如图,在△ABC中,∠C=90°,∠CAB,∠CBA的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:
如图,在△ABC中,∠C=90°,∠CAB,∠CBA的平分线相交于点D,DE⊥BC于点E,DF⊥AC于点F,求证:(1)四边形CFDE是矩形;
(2)四边形CFDE是菱形.
分析 (1)根据垂直定义得出∠C=∠CFD=∠DEC=90°,根据矩形的判定推出即可;
(2)根据角平分线性质求出DE=DF,根据菱形的判定推出即可.
解答 证明:(1)∵DE⊥BC,DF⊥AC,∠C=90°,
∴∠C=∠CFD=∠DEC=90°,
∴四边形CFDE是矩形;
(2)如图,过D作DM⊥AB于M,
∵∠CAB,∠CBA的平分线相交于点D,DE⊥BC,DF⊥AC,
∴DE=DM,DM=DF,
∴DE=DF,
∵四边形CFDE是矩形,
∴四边形CFDE是菱形.
点评 本题考查了矩形的判定,菱形的判定,角平分线性质的应用,能运用定理进行推理是解此题的关键,注意:三个角都是直角的四边形是矩形,有一组邻边相等的平行四边形是菱形,难度适中.

练习册系列答案
相关题目
4.-32的相反数是( )
| A. | 9 | B. | -9 | C. | 6 | D. | -6 |
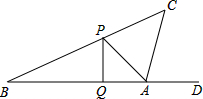 2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上.
2015年 4月18日潍坊国际风筝节拉开了帷幕,这天小敏同学正在公园广场上放风筝,如图风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小亮同学,发现自己的位置与风筝和广场边旗杆PQ的顶点P在同一直线上. 如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.
如图,△ABC中,以AB为直径的⊙O交AC于D,已知CD=AD.