Question

11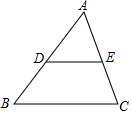．如图，在△ABC中，D、E为边AB、AC的中点，已知△ADE的面积为4，那么△ABC的面积是16．

Answer 1

分析 根据三角形的中位线定理求出DE=$\frac{1}{2}$BC，DE∥BC，求出△ADE∽△ABC，根据相似三角形的性质得出比例式，代入求出即可．

解答 解：∵D、E为边AB、AC的中点，
∴DE=$\frac{1}{2}$BC，DE∥BC，
∴△ADE∽△ABC，
∴$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=（$\frac{DE}{BC}$）²=$\frac{1}{4}$，
∵△ADE的面积为4，
∴△ABC的面积是16，
故答案为：16．

点评 本题考查了相似三角形的性质和判定，三角形的中位线定理等知识点，能推出△ADE∽△ABC是解此题的关键，注意：相似三角形的面积比等于相似比的平方．