题目内容
6.在一个不透明的盒子中装有14个白球,若干个黄球,这些球除颜色外都相同,若从中随机摸出一个球是白球的概率是$\frac{1}{3}$,则黄球的个数为28个.分析 设黄球的个数为x,根据概率公式列出方程,求出x的值即可.
解答 解:设黄球的个数为x,根据题意得:
$\frac{14}{14+x}$=$\frac{1}{3}$,
解得:x=28,
答:黄球的个数为28个;
故答案为:28.
点评 此题主要考查了概率公式的应用,用到的知识点为:概率=所求情况数与总情况数之比.得到所求的情况数是解决本题的关键.

练习册系列答案
相关题目
1.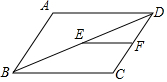 如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
 如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )
如图,在?ABCD中,AD=7,点E、F分别是BD、CD的中点,则EF等于( )| A. | 2.5 | B. | 3 | C. | 4 | D. | 3.5 |
15. 如图,在△ABC中,∠A=40°,∠B=60°,CD⊥AB于点D,CE平分∠ACD,DF⊥CE于点F,则∠CDF的度数为( )
如图,在△ABC中,∠A=40°,∠B=60°,CD⊥AB于点D,CE平分∠ACD,DF⊥CE于点F,则∠CDF的度数为( )
 如图,在△ABC中,∠A=40°,∠B=60°,CD⊥AB于点D,CE平分∠ACD,DF⊥CE于点F,则∠CDF的度数为( )
如图,在△ABC中,∠A=40°,∠B=60°,CD⊥AB于点D,CE平分∠ACD,DF⊥CE于点F,则∠CDF的度数为( )| A. | 70° | B. | 80° | C. | 85° | D. | 78° |
16.与$\sqrt{3}$是同类二次根式的为( )
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{30}$ |
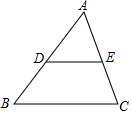 如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16.
如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16.