题目内容
2.以Rt△ABC的锐角顶点A为圆心,适当长为半径作弧,与边AB,AC各相交于一点,再分别以这两个交点为圆心,适当长为半径作弧,过两弧的交点与点A作直线,与边BC交于点D.若∠ADB=60°,点D到AC的距离为2,则AB的长为2$\sqrt{3}$.分析 如图,作DE⊥AC于E.首先证明BD=DE=2,在Rt△ABD中,解直角三角形即可解决问题.
解答 解:如图,作DE⊥AC于E.
由题意AD平分∠BAC,
∵DB⊥AB,DE⊥AC,
∴DB=DE=2,
在Rt△ADB中,∵∠B=90°,∠BDA=60°,BD=2,
∴AB=BD•tan60°=2$\sqrt{3}$,
故答案为2$\sqrt{3}$
点评 本题考查作图-基本作图,角平分线的性质定理、锐角三角函数等知识,解题的关键是熟练掌握角平分线的性质定理,属于中考常考题型.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
13.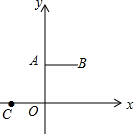 如图,已知点A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上.若抛物线与线段AB无公共点,则k的取值范围是( )
如图,已知点A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上.若抛物线与线段AB无公共点,则k的取值范围是( )
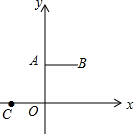 如图,已知点A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上.若抛物线与线段AB无公共点,则k的取值范围是( )
如图,已知点A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上.若抛物线与线段AB无公共点,则k的取值范围是( )| A. | 0<k<2 | B. | 0<k<2或k>$\frac{8}{3}$ | C. | k>$\sqrt{7}$ | D. | 0<k<2或k>$\sqrt{7}$ |
10.下列计算结果是x6的是( )
| A. | x2•x3 | B. | x2+x3 | C. | x12÷x2 | D. | (x2)3 |
7.一个圆锥的侧面展开图是圆心角为120°且半径为6的扇形,则这个圆锥的底面半径为( )
| A. | 1.5 | B. | 2 | C. | 2.5 | D. | 3 |
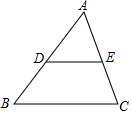 如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16.
如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16. 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.
如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.