题目内容
1.计算:($\sqrt{48}$+$\sqrt{3}$)÷$\sqrt{27}$=$\frac{5}{3}$.分析 先把二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.
解答 解:原式=(4$\sqrt{3}$+$\sqrt{3}$)÷3$\sqrt{3}$
=5$\sqrt{3}$÷3$\sqrt{3}$
=$\frac{5}{3}$.
故答案为=$\frac{5}{3}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.

练习册系列答案
相关题目
9.某种药品两次降价后,每盒从25元降到16元,则平均每次降价的百分率是( )
| A. | 10% | B. | 20% | C. | 25% | D. | 30% |
16.与$\sqrt{3}$是同类二次根式的为( )
| A. | $\sqrt{18}$ | B. | $\sqrt{\frac{1}{3}}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\sqrt{30}$ |
6.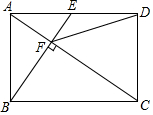 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$,其中正确的结论有( )| A. | ①②④ | B. | ①②③ | C. | ②③④ | D. | ①③④ |
13.已知变量s与t的关系式是s=6t-$\frac{5}{2}$t2,则当t=2时,s=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
10.已知$\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{mx+ny=8}\\{nx-my=1}\end{array}\right.$的解,则2m+n的立方根为( )
| A. | 4 | B. | 2 | C. | $\sqrt{2}$ | D. | ±2 |
11.下列各式,能用平方差公式计算的是( )
| A. | (a+b)(-a-b) | B. | (a+b)(-a+b) | C. | (-a+b)(a-b) | D. | (-a+b)(b-a) |
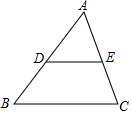 如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16.
如图,在△ABC中,D、E为边AB、AC的中点,已知△ADE的面积为4,那么△ABC的面积是16. 如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.
如图,直线AB,CD相交于点O,若∠AOC+∠BOD=90°,则∠BOC的度数为135°.