��Ŀ����
1����x1��x2�����з��̵�����������������±���| ���� | x1 | x2 | x1+x2 | x1•x2 |
| x2-5x+4=0 | 1 | 4 | 5 | 4 |
| x2+7x+12=0 | -3 | -4 | -7 | 12 |
| x2-4x-5=0 | 5 | -1 | 4 | -5 |
| x2+bx+c=0 | $\frac{-b+\sqrt{{b}^{2}-4c}}{2}$ | $\frac{-b-\sqrt{{b}^{2}-4c}}{2}$ | -b | c |
��2�����������㷢�ֵĽ��ۣ������������⣺��֪����x2+3x-5=0���������ֱ�Ϊx1��x2 ��$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$��ֵ��
���� �ֱ�ⷽ����ɱ���
��1�����ñ����е����ݿɵõ���x1��x2��һԪ���η���ax2+bx+c=0��a��0��������ʱ��x1+x2=-$\frac{b}{a}$��x1x2=$\frac{c}{a}$��
��2�����ã�1���н��۵�x1+x2=-3��x1x2=-5��Ȼ��ͨ�ֵõ�$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$���������������ķ������㣮
��� �⣺��1�����ۣ���x1��x2��һԪ���η���ax2+bx+c=0��a��0��������ʱ��x1+x2=-$\frac{b}{a}$��x1x2=$\frac{c}{a}$��
��2�����ã�1���н��۵�x1+x2=-3��x1x2=-5��
����$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}{x}_{2}}$=$\frac{-3}{-5}$=$\frac{3}{5}$��
�ʴ�Ϊ1��4��5��4��-3��-4��-7��12��5��-1��4��-5��$\frac{-b+\sqrt{{b}^{2}-4c}}{2}$��$\frac{-b-\sqrt{{b}^{2}-4c}}{2}$��-b��c��
���� ���⿼���˸���ϵ���Ĺ�ϵ����x1��x2��һԪ���η���ax2+bx+c=0��a��0��������ʱ��x1+x2=-$\frac{b}{a}$��x1x2=$\frac{c}{a}$��

 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�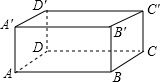 ��һ��������ֽ�У����������߷ֱ�Ϊ4cm��3cm��12cm��������һ�㣬�ܷ��һ����Ϊ18cm��Ǧ�ʷ������ֽ�����棿
��һ��������ֽ�У����������߷ֱ�Ϊ4cm��3cm��12cm��������һ�㣬�ܷ��һ����Ϊ18cm��Ǧ�ʷ������ֽ�����棿