题目内容
8.已知xy=3,求x$\sqrt{\frac{y}{x}}$+y$\sqrt{\frac{x}{y}}$的值.分析 根据题意得出x,y同号,再利用x,y同为正数或负数进而化简二次根式求出即可.
解答 解:∵xy=3,
∴x,y同号,
当x,y同为正数,
∴$\sqrt{\frac{y}{x}}$+y$\sqrt{\frac{x}{y}}$=x$\sqrt{\frac{xy}{{x}^{2}}}$+y$\sqrt{\frac{xy}{{y}^{2}}}$=$\sqrt{xy}$+$\sqrt{xy}$=$\sqrt{3}$+$\sqrt{3}$=2$\sqrt{3}$;
当x,y同为负数,
∴$\sqrt{\frac{y}{x}}$+y$\sqrt{\frac{x}{y}}$=x$\sqrt{\frac{xy}{{x}^{2}}}$+y$\sqrt{\frac{xy}{{y}^{2}}}$=-$\sqrt{xy}$-$\sqrt{xy}$=-$\sqrt{3}$-$\sqrt{3}$=-2$\sqrt{3}$.
点评 此题主要考查了二次根式的化简求值,正确分类讨论得出是解题关键.

练习册系列答案
相关题目
17.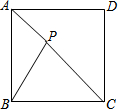 如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
 如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )
如图,P为正方形内一点,若PA:PB:PC=1:2:3,则∠APB的度数是( )| A. | 120° | B. | 135° | C. | 145° | D. | 150° |
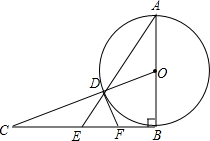 如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点.
如图,AB=BC,∠ABC=90°,以AB为直径的⊙O交OC于点D,AD的延长线交BC于点E,点F为BE的中点. 如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.
如图,点A是抛物线C1:y=$\frac{1}{2}$x2+2x+1的顶点,点B是抛物线C2:y=$\frac{1}{2}$x2+bx+c的顶点,并且OB⊥OA.